The computation, visualization, and interpretation of brain variability remains a significant challenge in computational neuroanatomy. Current deformable registration methods can generate, for each vertex of a polygonal mesh modeling the cortical surface, a distribution of displacement vectors between the individual models and their average, which can be summarized as a covariance tensor. While analysis of anatomical covariance tensor fields promises insight into the structural components of aging and disease, basic understanding of the tensor field structure is hampered by the lack of effective methods to create informative and interactive visualizations. We describe a novel application of superquadric tensor glyphs to anatomic covariance tensor fields, supplemented by colormaps of important tensor attributes. The resulting visualizations support a more detailed characterization of population variability of brain structure than possible with previous methods, while also suggesting directions for subsequent quantitative analysis.
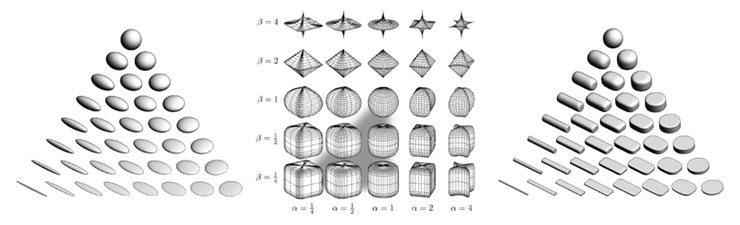 Figure 1: (a) Ellipsoid tensor glyphs, (b) Space of superquadrics, (c) Superquadric tensor glyphs. Ellipsoidal glyphs (a) suffer from visual ambiguity. The range of superquadrics (b) used for tensor glyphs is highlighted with the gray triangle. Superquadric glyphs (c) differentiate shape and convey orientation more clearly than do ellipsoids. Figure 1: (a) Ellipsoid tensor glyphs, (b) Space of superquadrics, (c) Superquadric tensor glyphs. Ellipsoidal glyphs (a) suffer from visual ambiguity. The range of superquadrics (b) used for tensor glyphs is highlighted with the gray triangle. Superquadric glyphs (c) differentiate shape and convey orientation more clearly than do ellipsoids. |
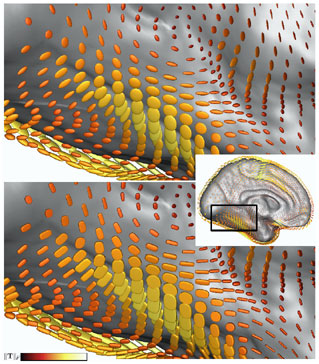 Figure 2: Comparison of ellipsoid (top) and superquadric (bottom) glyphs, colormapped with ||T||F Figure 2: Comparison of ellipsoid (top) and superquadric (bottom) glyphs, colormapped with ||T||F |
This work represents anatomic variability as a field of covariance tensors over the cortical surface. In general, the challenge of tensor visualization is to convey the properties of individual tensor samples, as well as the large-scale spatial structure of changes in the tensor attributes, in such a way that does not overwhelm the viewer with an unintelligible mass of information. When visualizing covariance data computed from deformable registration of cortical surface models, we require the ability to inspect the degree and type of population variance at particular locations of interest on the cortical surface (such as the language areas of the brain in Alzheimer's disease), as well as the means of discerning overall patterns of variation that may represent novel indicators for biologically significant subpopulation characteristics.
We are exploring the combination of superquadric tensor glyphs and judicious application of colormaps to display individual tensors and the spatial structure of the tensor field, respectively. Glyphs, or icons, depict multiple data values by mapping them onto the shape, size, orientation, and surface appearance of a base geometric primitive. Tensor glyphs generally indicate the tensor eigenvalues and eigenvectors by their scaling (shape) and orientation, respectively, as with the ellipsoidal glyphs commonly used to present diffusion tensor MRI data. The limited previous work in visualizing anatomic covariance tensor fields employed nested semi-transparent ellipsoidal glyphs corresponding to a small set of confidence limits.
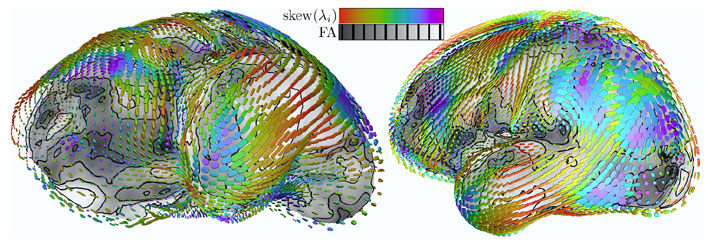 Figure 3: Eigenvalue skew colormapped on glyphs, fractional anisotropy on cortical surface. Sequence of quantities colormapped on superquadric glyphs, with gray-scale indication on the underlying mesh surface. Figure 3: Eigenvalue skew colormapped on glyphs, fractional anisotropy on cortical surface. Sequence of quantities colormapped on superquadric glyphs, with gray-scale indication on the underlying mesh surface. |