Approximating the Generalized Voronoi Diagram of Closely Spaced Objects
1SCI Institute, University of Utah 2Google, Inc. 3The University of Texas

Abstract
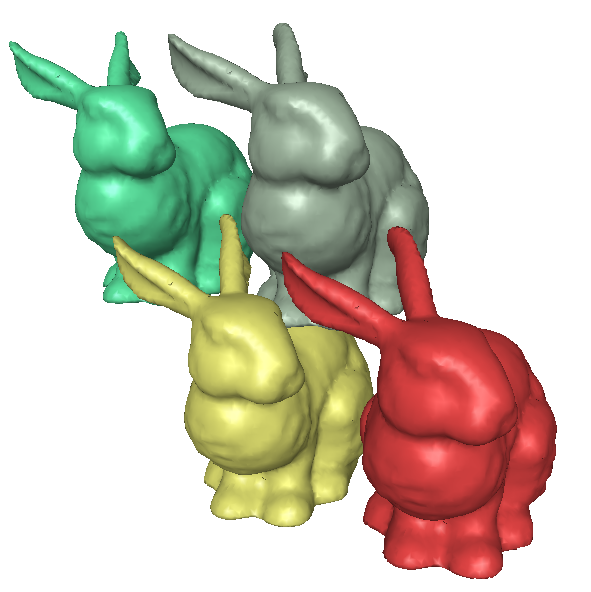
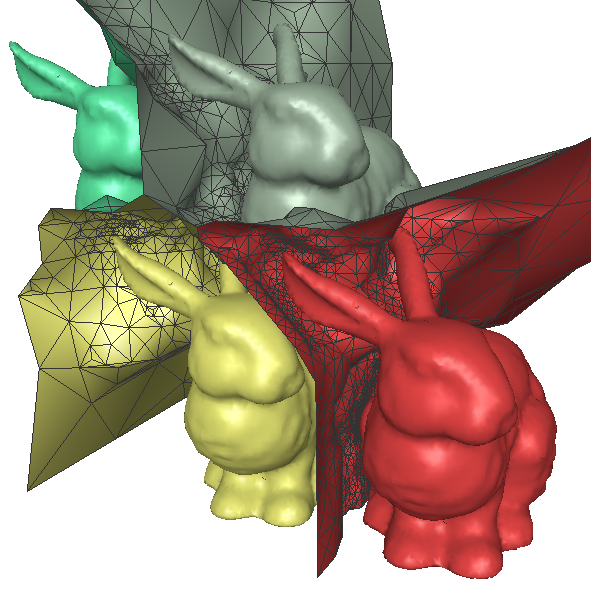
Generalized Voronoi Diagrams (GVDs) have far-reaching applications in robotics, visualization, graphics, and simulation. However, while the ordinary Voronoi Diagram has mature and efficient algorithms for its computation, the GVD is difficult to compute in general, and in fact, has only approximation algorithms for anything but the simplest of datasets. Our work is focused on developing algorithms to compute the GVD efficiently and with bounded error on the most difficult of datasets -- those with objects that are extremely close to each other.
BibTeX
@article{edwards2015approximating,
author = "John Edwards and Eric Daniel and Valerio Pascucci and Chandrajit Bajaj",
title = "Approximating the Generalized Voronoi Diagram of Closely Spaced Objects",
journal = {Computer Graphics Forum (Eurographics 2015)},
year = 2015
}
Funding
The work of JE and VP was supported in part by NSF IIS-1314896, NSF ACI-0904631, DOE/NEUP 120341, DOE/UV-CDAT DESC0006872, DOE/Codesign P01180734, DOE/SciDAC DESC0007446, DOE/PIPER DESC0010498, and DOE/CCMSC DENA0002375. This work initiated at the University of Texas when JE, ED and CB were supported in part by NIH contract R01-EB00487, NSF Grant OCI-1216701 and SNL contract 1439100.