|
|
|
|
|
|
|
|
|
Award Number and Duration |
|
|
|
NSF DMS 2301361 (University of Utah)
Collaborating Projects: |
|
|
|
PIs |
|
|
|
Bei Wang (University of Utah, PI)
Facundo Mémoli (OSU, PI)
Tamal Dey (Perdue University, PI) |
|
|
|
Collaborators |
|
|
|
Kelin Xia, Associate Professor, School of Physical & Mathematical Sciences, Nanyang Technological University. |
|
|
|
Overview |
|
|
|
Complex datasets arise in many disciplines of science and engineering and require multiparameter data analysis, which broadly speaking, studies the dependency of a phenomenon or a space on multiple parameters. In recent years, topological data analysis (TDA) has evolved as an emerging area in data science. So far, most of its applications have been limited to the single parameter case, that is, to data expressing the behavior of a single variable. As its reach to applications expands, the task of extracting intelligent summaries out of diverse, complex data demands the study of multiparameter dependencies. This project will help address this demand. |
|
|
|
Broader Impacts |
|
|
|
This project will develop a sound mathematical theory supported by efficient algorithmic tools for the aforementioned thrusts and, thus, will provide a powerful platform for data exploration and analysis in a range of applications in science and engineering. The educational impact will be accelerated by the synergy between mathematics and computer science and integrated applications. Graduate students supported by the project will be trained to: develop skills in mathematics and theoretical computer science, most notably in algorithms and topology, write efficient and usable software, and analyze real-world data sets. The PIs will provide best practice recruiting and mentoring of students from underrepresented groups. The PIs plan to broaden research engagement via workshops or tutorials at computational topology and TDA venues. A nationally focused hackathon will introduce methodologies and software tools for multiparameter TDA to the research community as where participants work on data analysis projects while being mentored by disciplinary experts. The outreach activities including a K-12 summer camp and a data science day will further converge disciplinary communities and introduce high school students to novel modern data analysis. |
|
|
|
Publications and Manuscripts |
|
|
| Manuscripts | |
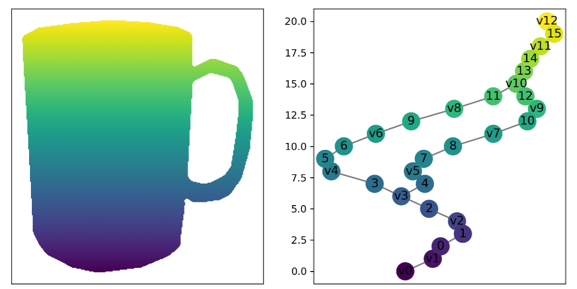
|
 Towards an Optimal Bound for the Interleaving Distance on Mapper Graphs.
Towards an Optimal Bound for the Interleaving Distance on Mapper Graphs.
Erin Wolf Chambers, Ishika Ghosh, Elizabeth Munch, Sarah Percival, Bei Wang. Manuscript, 2025. arXiv:2504.03865 |
|
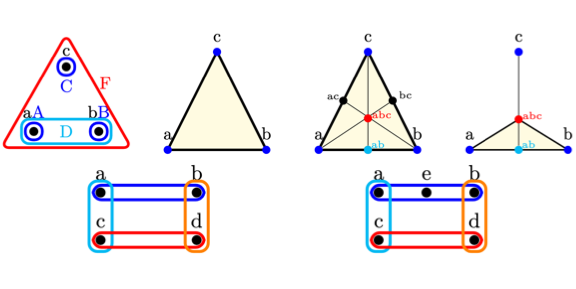
 A Survey of Simplicial, Relative, and Chain Complex Homology Theories for Hypergraphs.
A Survey of Simplicial, Relative, and Chain Complex Homology Theories for Hypergraphs.
Ellen Gasparovic, Emilie Purvine, Radmila Sazdanovic, Bei Wang, Yusu Wang, Lori Ziegelmeier. Manuscript, 2024. arXiv:2409.18310 |
| Year 2 (2023-2024) | |

|
 Structural Uncertainty Visualization of Morse Complexes for Time-Varying Data Prediction.
Structural Uncertainty Visualization of Morse Complexes for Time-Varying Data Prediction.
Weiran Lyu, Saumya Gupta, Chao Chen, Bei Wang. IEEE Workshop on Topological Data Analysis and Visualization (TopoInVis) at IEEE VIS, 2025. |

|
 Extracting Complex Topology from Multivariate Functional Approximation: Contours, Jacobi Sets, and Ridge-Valley Graphs.
Extracting Complex Topology from Multivariate Functional Approximation: Contours, Jacobi Sets, and Ridge-Valley Graphs.
Guanqun Ma, David Lenz, Hanqi Guo, Tom Peterka, Bei Wang. IEEE Symposium on Large Data Analysis and Visualization (LDAV), 2025. Supplement. |
|
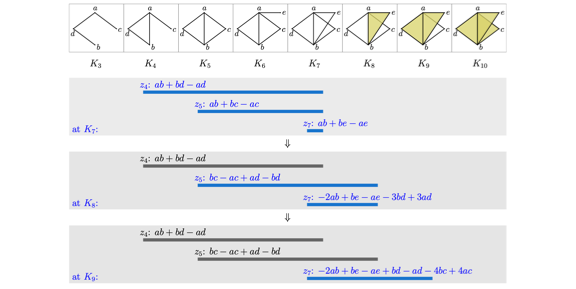
 Tracking the Persistence of Harmonic Chains: Barcode and
Stability.
Tracking the Persistence of Harmonic Chains: Barcode and
Stability.
Tao Hou, Salman Parsa, Bei Wang. International Symposium on Computational Geometry (SOCG), 2025. DOI: 10.4230/LIPIcs.SoCG.2025.58 arXiv:2412.15419. |

|
 Bounding the Interleaving Distance for Mapper Graphs with a Loss
Function.
Bounding the Interleaving Distance for Mapper Graphs with a Loss
Function.
Erin W. Chambers, Elizabeth Munch, Sarah Percival, Bei Wang. Journal of Applied and Computational Topology, 9, article number 19, 2025. DOI: 10.1007/s41468-025-00215-x Download online arXiv:2307.15130 |
|
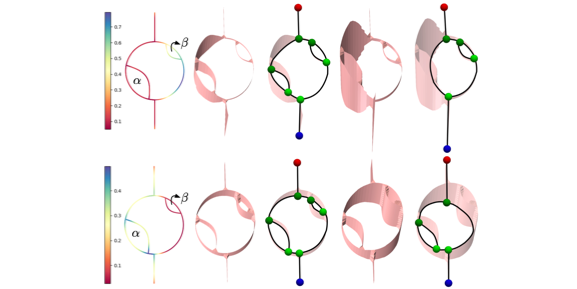
 Measure-Theoretic Reeb Graphs and Reeb Spaces.
Measure-Theoretic Reeb Graphs and Reeb Spaces.
Qingsong Wang, Guanqun Ma, Raghavendra Sridharamurthy, Bei Wang. Discrete & Computational Geometry (DCG), minor revision, 2025. arXiv:2401.06748. |
|
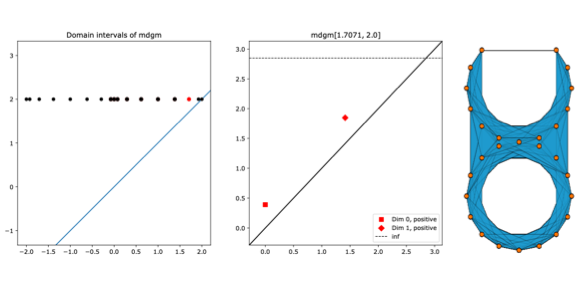
 Meta-Diagrams for 2-Parameter Persistence.
Nate Clause, Tamal K. Dey, Facundo Mémoli, Bei Wang.
Meta-Diagrams for 2-Parameter Persistence.
Nate Clause, Tamal K. Dey, Facundo Mémoli, Bei Wang.
Discrete & Computational Geometry (DCG), 2025. DOI: 10.1007/s00454-025-00741-6 |
|
 Finding the Cores of Higher Graphs Using Geometric and Topological Means: A Survey.
Inés García-Redondo, Claudia Landi, Sarah Percival, Anda Skeja, Bei Wang, Ling Zhou.
Finding the Cores of Higher Graphs Using Geometric and Topological Means: A Survey.
Inés García-Redondo, Claudia Landi, Sarah Percival, Anda Skeja, Bei Wang, Ling Zhou.
Research in Computational Topology 3, Association for Women in Mathematics Series, Springer, Cham, accepted, 2025. |
| Year 1 (2023 - 2024) | |
|
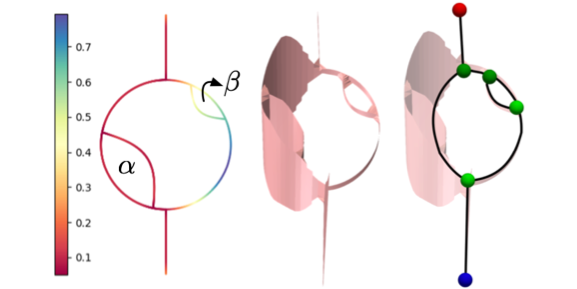
 Measure-Theoretic Reeb Graphs and Reeb Spaces.
Measure-Theoretic Reeb Graphs and Reeb Spaces.
Qingsong Wang, Guanquan Ma, Raghavendra Sridharamurthy, Bei Wang. International Symposium on Computational Geometry (SOCG), 2024. DOI:10.4230/LIPIcs.SoCG.2024.80 arXiv:2401.06748. |

|
 PersiSort: A New Perspective on Adaptive Sorting Based on Persistence.
PersiSort: A New Perspective on Adaptive Sorting Based on Persistence.
Jens Kristian Refsgaard Schou, Bei Wang. Proceedings of the 36th Canadian Conference on Computational Geometry (CCCG), 2024. |

|
 Computing Loss Function to Bound the Interleaving Distance for Mapper Graphs (Abstract).
Computing Loss Function to Bound the Interleaving Distance for Mapper Graphs (Abstract).
Erin Wolf Chambers, Ishika Ghosh, Elizabeth Munch, Sarah Percival, Bei Wang. International Symposium on Computational Geometry (SOCG) Young Researcher Forum (YRF), 2024. |
|
|
|
Presentations, Educational Development and Broader Impacts |
|
|
| Year 2 (2024 - 2025) |
|
| Year 1 (2023 - 2024) |
|
|
|
|
Postdocs and Students |
|
|
|
Current Students:
Former Students and Postdocs: |
|
|
|
Acknowledgement |
|
|
|
This material is based upon work supported or partially supported by the National Science Foundation under Grant No. 2301361. |
|
|