Computational Topology with Applications
Valerio Pascucci & Pavol Klacansky & Aravinda Kanchana Ruwanpathirana
Class
Information:
|
Term |
Number |
Subject |
Catalog # |
Section |
Days |
Time |
Location |
Office |
|
Spring 2024 |
20012 |
CS |
002 |
Monday, |
8:05 AM |
WEB L122 |
TBD |
Course Overview. This course provides a gentle introduction to topology-based techniques for the analysis and visualization of geometric models and unstructured data. Students will learn about fundamental topological invariants (connectedness, Euler characteristic, orientability, etc…) and constructs (Reeb graphs, Morse-Smale complexes, Jacobi Sets, etc…), as well as efficient algorithms for their computation and their use in a Machine Learning context. Special emphasis will be given to the analysis of the algorithms with respect to (i) asymptotic complexity, (ii) robustness, (iii) data structures and implementation issues, (iv) domain-specific data analytics, and (v) visual insight and user interfaces for general purpose data exploration. The practical use of the techniques presented in class will be demonstrated for the analysis of geometric models commonly used in Computer Graphics and Scientific Visualization. Whenever possible, reference implementation is Python, and Jupyter Notebooks will be used. Successful completion of the course will enable the students to apply Topological Data Analysis (TDA) to the solution of data analysis problems in science and engineering, to pursue new research directions in TDA, or to apply the most recent topological techniques to related areas such as computer graphics, geometric modeling, meshing, and scientific visualization.
Prerequisites. There are no formal prerequisites for this class. Students will be expected to have basic knowledge of geometric data structures and algorithmic techniques and basic programming experience in Python (or equivalent).
Tentative
Syllabus (changes based on student feedback will be considered):
|
|
Graphs and Connected Components |
Manifolds and Orientability |
Simplicial Complexes |
|
January 8, 2024 |
January 10, 2024 |
January 17, 2024 |
January 22, 2024 |
|
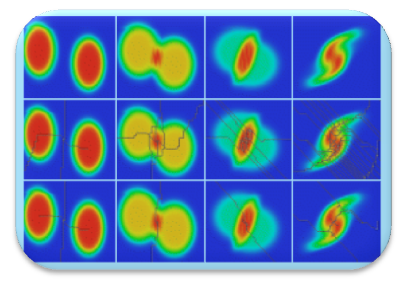
Betti Numbers
|
Smith Normal Form January 29, 2024 |
(PL) Morse Functions and transversality January 31, 2024 |
February 5, 2024 |
|
February 7, 2024 |
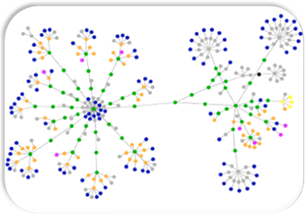
Contour Trees in nD February 12, 2024 |
Topological Simplification February 14, 2024 |
Contour Trees February 21, 2024 |
|
of Morse Functions February 26, 2024 |
Dynamic Contour Trees February 28, 2024 |
|
|
|
Midterm On paper, in class March 11, 2024 |
Machine Learning and TDA: Mapper Basics March 13, 2024 |
Machine Learning and TDA Mapper in High Dimensions March 18, 2024 |
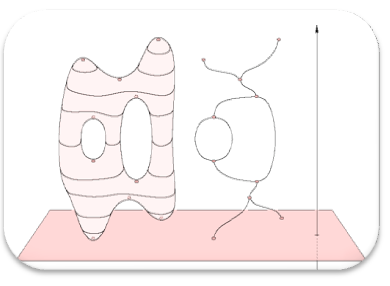
2D Morse-Smale Complex March 20, 2024 |
|
Hierarchical 2D Morse-Smale Complex March 25, 2024 |
3D Morse-Smale Complex March 27, 2024 |
April 1, 2024 |
Robustness and Simulation of Simplicity April 3, 2024 |
|
and Voronoi Diagrams April 8, 2024 |
Alpha Complex and Alpha Shapes April 10, 2024 |
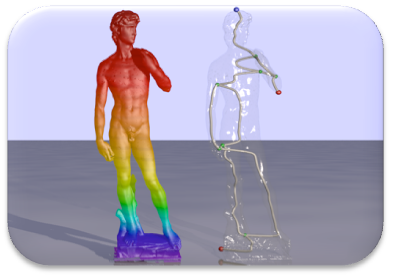
Morse Theory April 5, 2024 |
Morse-Smale Complexes April 17, 2024 |
|
Data Exploration April 22, 2024 |
|
Runtime Memory References |
Materials Under Stress |
|
|
|
from micro-CT scans |
Final
Project Presentation (all day): April 24 (or TBD), 2024 |
Reading and supplemental material
There is no formal book for class. The instructor will distribute on canvas printouts of notes or research papers related to each lecture.
The following links include various relevant materials such as book, research papers, and software:
· Main Book:
o Computational Topology by H. Edelsbrunner and J. Harer
· Other Books:
o Topology (2nd Edition) by J. Munkres
o Morse Theory by J. Milnor
o Combinatorial Topology by P. S. Alexandrov
o An Introduction to Morse Theory by Y. Matsumoto
· Jupyter Notebooks and Friends:
o Scikit-TDA is a home for Topological Data Analysis Python libraries intended for non-topologists
o GUDHI Geometry Understanding in Higher Dimensions
o Perseus Software Project for Rapid Computation of Persistent Homology
· Othe Information on the Web:
o Computational Geometry Pages by J. Erickson
o GemDir by E. Mücke
o CGAL
Assignments
The students will be given individual and group assignments. The main assignment will be a project. Although the students may be provided with a list of available projects, the students are highly encouraged to propose projects in areas of personal interest. For larger projects, the students may be allowed to work in small groups.
Late Submission of Assignments
Assignments will not be accepted late. Students will be given a one-time two-day extension for an unexpected event.
Class Participation and Absences
Participation in class is an integral part of the course.
Attendance is mandatory.
More than two unjustified absences will impact negatively the grade.
Grading
Each student will be evaluated based on:
· Attendance and participation in class (10%),
· Assignments (40%),
· Project (35%),
· Final project presentation (15%).
Course Policies
A detailed overview of the course policies can be found on: CS 6170- Course Policies
Students With Disabilities
The University of Utah seeks to provide equal access to its programs, services and activities for people with disabilities. If you will need accommodations in the class, reasonable prior notice needs to be given to the Center for Disability Services, 162 Olpin Union Building, 581-5020 (V/TDD). CDS will work with you and the instructor to make arrangements for accommodations. All written information in this course can be made available in alternative format with prior notification to the Center for Disability Services.