Computing and Visualizing Electric Potentials and Current Pathways in the Thorax

Quan Ni, - Robert S. MacLeod, - Bonnie B. Punske, - Bruno Taccardi

From Nora Eccles Harrison Cardiovascular Research and Training Institute,
University of Utah, Salt Lake City, Utah

Presented at the 2000 International Society for Computerized Electrocardiography Conference, Yosemite, CA.

Support:

Richard A. and Nora Eccles Harrison Treadwell Fund for Cardiovascular Research and awards from the Nora Eccles Treadwell Foundation, the Whitaker Foundation. National Institutes of Health SCOR in Sudden Cardiac Death, HL 52338-05.

Abstract

The long term goal of electrocardiography is to relate electric potential on the body surface with activities in the heart. Many previously reported studies have focused on direct links between heart and body surface potentials. The goals of this study were first to validate computational methods of determining volume potentials and currents with high-resolution experimental measurements and then to use interactive visualization of thoracic currents to understand features of the electrocardiographic fields from measured cardiac sources. We developed both simulation and experimental studies based on a realistically shaped torso phantom containing an isolated, perfused dog heart. Interventions included atrial pacing, single pacing and simultaneously pacing at multiple locations on the ventricles. Simulated torso volume potentials closely matched measured potentials in the torso-tank preparation (mean correlation coefficients of 0.95). Simulation further provided a means of estimating the current field in the torso from the computed torso volume potentials and the local geometric and conductive properties of the medium. Applying these techniques to the torso electric fields under a variety of pacing conditions, we have further demonstrated that thoracic current can provide many insights into the relationship between heart surface potential and body surface potentials. Specifically, we have shown that geometric factors including cardiac source configuration and location play an important role in determining to what extent electric activity in the heart is directly visible on the body surface electrocardiogram. The computation and visualization toolkit we developed in this study to explore current fields associated with cardiac events may provide new insights into electrocardiology.

Thoracic Potentials and Currents Quan Ni

Introduction

The long term goal of electrocardiography is to relate electric potential on the body surface with activities in the heart. Using potentials on the epicardial surface as a way to characterize cardiac electrical activities, many experimental[1,2] and theoretical studies[3,4,5] have focused on direct links between heart and body surface potentials. Spach et al. in their studies[1] of simultaneously measured epicardial and torso surface potentials on chimpanzee recognized that both cardiac sources (magnitude and configuration) and their location with respect to surface recording electrodes affected body surface electrocardiograms (ECG's). Theoretical studies[6,7] based on derivation of body surface potentials from heart potentials (forward solution) and vice versa (inverse solution) further demonstrated the ``smoothing'' effect of the volume conductor in projecting cardiac activities onto the torso surface. However, due to the lack of information about torso volume potentials, these studies could only speculate as to the causal links between cardiac sources and body surface potential distribution.

While measurements of cardiac bioelectric activity are usually based on electric potentials at the heart and body surfaces, it is the electric potential and current fields in the torso volume that are the physical connection between cardiac and body surface potentials. De Ambroggi and Taccardi studied the current and potential field from single and double dipoles placed in a simplified, two-dimensional physical model of the volume conductor in great detail and used their results to illustrate features of the boundary (body surface) potentials that could identify features of the actual sources.[8] Colli-Franzone et al.[9] used the volume potential field in a cylindrical torso model to study the role of tissue anisotropy. In addition, Johnson et al. in a series of modeling studies[10,11,12] demonstrated the use of simulated thoracic current fields in studying the role of the volume conductor in electrocardiography. In all these studies, the goal was similar: to examine the electric potential and current fields within the volume conductor in order to understand the relationship between cardiac sources and the body-surface electrocardiogram.

The goals of this study were first to validate computational methods of determining volume potentials and currents with high-resolution experimental measurements and then to use interactive visualization of thoracic currents to understand features of the electrocardiographic fields from measured cardiac sources. We developed both simulation and experimental studies based on a realistically shaped torso phantom containing an isolated, perfused dog heart. Our simulations of torso bioelectric fields with input of measurements on the heart, unlike those in many previously reported studies, were aimed at reproducing potential and current fields observed in physiological conditions of the heart under atrial and ventricular pacing. Simulated torso volume potentials were validated directly by experimental measurements. A specific aim of this study was to investigate the influence of the geometric configuration of cardiac sources on the distribution of electric current pathways in the thorax.

Methods

The methods required for this study involved computation and visualization of current flows in the torso volume. To this end, we developed simulation techniques to compute volume potentials in the form of a numerical solution to the forward problem of electrocardiography, and then estimate current from the electric potentials. In addition, we used an experimental preparation, which consisted of a perfused isolated heart suspended in a torso-shaped tank, to provide input and validation data for the simulations. Finally, we employed customized visualization tools to interpret simulated torso volume potential and current distributions.

Computational Methods

Computation of Potential Distributions in the Thorax

In the volume conductor ( $\Omega$ ) bounded by the heart and body surfaces, electric potentials obey Laplace's equation

$\displaystyle \nabla$ ^.( $\displaystyle \sigma$ $\displaystyle \nabla$ $\displaystyle \Phi$ ) = 0, in $\displaystyle \Omega$ ,

(1)

subject to boundary conditions

$\displaystyle \Phi$ = $\displaystyle \Phi_{0}^{}$ on $\displaystyle \Gamma_{H}^{}$

(2)

and

$\displaystyle \sigma$ $\displaystyle \nabla$ $\displaystyle \Phi$ ^. $\displaystyle \bf n$ = 0 on $\displaystyle \Gamma_{B}^{}$ .

(3)

$\Phi_{0}^{}$ is the potential at a set of locations on the surface of heart ( $\Gamma_{H}^{}$ ), known a priori; n is an outward unit normal vector to the body surface ( $\Gamma_{B}^{}$ ). $\sigma$ is the conductivity tensor, which reduces to a scalar in a homogeneous conducting medium.

We solved Equation (1) numerically using the finite element method (FEM) with a Garlerkin formulation, the details of which are available in many references, for example, Johnson[13]. Briefly, the volume conductor was discretized into tetrahedral elements over which potentials were approximated by a linear interpolation function. The result was a system of linear equations, A $\Phi$ = b, subjects to the boundary conditions in Equations (2) and (3). Here, A is the global stiffness matrix, which contains geometry and conductivity information, $\Phi$ is the solution vector of all potentials on the surfaces and at all nodes within the volume, and b is the load vector, which contains all zeros for Laplace's equation.

Traditionally, one applies the FEM for a single set of boundary conditions and solves the resulting system of equations. However, it is also possible to reformulate the solution in a way that allows its application to many sets of Dirichlet boundary conditions (in our case, epicardial potentials). To create this more useful formulation, we can partition the global stiffness matrix, A into submatrices according to local regions within the volume as:

$\displaystyle \left(\vphantom{ \begin{array}{ccc} A_{BB} & A_{BV} & A_{BH} \\ A_{VB} & A_{VV} & A_{VH} \\ A_{HB} & A_{VH} & A_{HH} \end{array} }\right.$ $\displaystyle \begin{array}{ccc} A_{BB} & A_{BV} & A_{BH} \\ A_{VB} & A_{VV} & A_{VH} \\ A_{HB} & A_{VH} & A_{HH} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccc} A_{BB} & A_{BV} & A_{BH} \\ A_{VB} & A_{VV} & A_{VH} \\ A_{HB} & A_{VH} & A_{HH} \end{array} }\right)$ $\displaystyle \left(\vphantom{ \begin{array}{c} \Phi_{B} \Phi_{V} \Phi_{H} \end{array}}\right.$ $\displaystyle \begin{array}{c} \Phi_{B} \Phi_{V} \Phi_{H} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{c} \Phi_{B} \Phi_{V} \Phi_{H} \end{array}}\right)$ = $\displaystyle \left(\vphantom{ \begin{array}{c} 0 0 0 \end{array} }\right.$ $\displaystyle \begin{array}{c} 0 0 0 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{c} 0 0 0 \end{array} }\right)$ with $\displaystyle \Phi$ = $\displaystyle \Phi_{0}^{}$ on $\displaystyle \Gamma_{H}^{}$ ,

(4)

where subscripts B, V, and H stand for body, volume, and heart respectively. From the above equations, come the following two equations that relate directly potentials in the volume and body surface with known potential values on the heart surface,

$\displaystyle \Phi_{B}^{}$	=	(A_BB - A_BVA_VV^-1A_VB)^-1(A_BVA_VV^-1A_VH - A_BH) $\displaystyle \Phi_{H}^{}$	(5)
$\displaystyle \Phi_{V}^{}$	=	- A_VV^-1(A_VH $\displaystyle \Phi_{H}^{}$ + A_VB $\displaystyle \Phi_{B}^{}$ ).	(6)

The above formulation is referred to as the forward problem in electrocardiography, whose solution is well-behaved and numerically well-conditioned. Thus, during the cardiac cycle, assuming static geometric configuration and conductivity in the volume conductor, we could compute the above forward transfer matrix once and reuse it for any sequence of known epicardial potentials by means of simple matrix-vector multiplications

$\displaystyle \Phi_{B}^{}$ = Z_BH $\displaystyle \Phi_{H}^{}$			(7)
$\displaystyle \Phi_{V}^{}$ = Z_VH $\displaystyle \Phi_{H}^{}$ ,			(8)

where Z_BH and Z_VH are transform matrices for the body surface and volume sites, respectively.

Computation of Thoracic Currents

Current density (J) within the volume conductor is defined as the product of the potential gradient, $\nabla$ $\Phi$ and conductivity, $\sigma$ ,

$\displaystyle \bf J$ = - $\displaystyle \sigma$ $\displaystyle \nabla$ $\displaystyle \Phi$ .

(9)

To estimate the spatial gradient of the potentials in the discrete geometric model of the thorax, we used a least square approximation technique.[14] For each evaluation point, we first fit potential values from nearby sites in the tetrahedral mesh with a tri-linear polynomial function and then used the spatial derivative of this function as an approximation of $\nabla$ $\Phi$ . The result was the current density as a vector field consisting of discrete values located at each evaluation point.

Three Dimensional Visualization Techniques

One challenge of evaluating thoracic currents--and three-dimensional fields generally--is in visualizing the data in a useful manner. For the three-dimensional potential distributions in the torso, we used a scalar field visualization technique called isosurface rendering, in which one identifies points of equal scalar value and connects them into a surface by means of triangles. The resulting ``iso-potential surfaces'' are the three-dimensional equivalent of the iso-potential contours used to display scalar fields in two-dimensional domains or over surfaces.

To visualize vector-valued fields in space, one common approach is to draw individual arrows to represent the current vector magnitude and direction at discrete sites, a technique sometimes referred to as ``quiver plots''. While this approach works reasonably well for vector fields with simple patterns, it often becomes cluttered or overwhelmingly complex in current fields such as those generated by the heart. To this end, we used a visualization technique known as streamlines for torso current distributions. In this method, each streamline follows a pathway of an imaginary particle placed in the vector field, in our case the path of a positive charge within the current field of the body. This requires first defining a set of seed points which are the start points of the particles within the volume, and then determining the local current vector for each seed point as described above. The next point on the streamline is then found by integrating the local current vector by a pre-determined integration step and then computing a new local current vector and continuing along the resulting pathway. The resulted streamlines trace the current paths in space, which is a direct analog of following the path of a physical particle in a flow field.[15]

For rendering of both isosurfaces and streamlines, we used a scientific problem solving environment called SCIRun, developed at the University of Utah.[16] For viewing potential distributions on the heart or body surface, we used our own custom visualization software.[17,18]

Experimental Methods

The experimental preparation consisted of an isolated dog heart, perfused by a second support dog and suspended in an torso-shaped tank. [19,20,5] The torso tank is a fiberglass shell in the shape of an adolescent thorax filled with electrolyte of conductivity (500 $\Omega$ ^.cm). The mapping system included 384 tank surface electrodes and 918 electrodes along 384 rods that projected from the tank surface into the volume toward the heart. The rods in the upper part of the tank were free to move in the radial direction. With the perfused, isolated heart suspended in the tank, the rods were pushed inward until their tips rested approximately 1 cm away from the epicardial surface. In the forward simulation, potentials on the rod tips close to the heart were used to represent epicardial potentials. The positions of the rod-tip electrodes were measured in the same frame of reference as the torso electrode, thus provided more controlled conditions for evaluating the simulation results. The acquisition system sampled potentials at 1 kHz with 12-bit resolution and a frequency response of 0.03 Hz and 500 Hz. Pacing was delivered with subepicardial electrode pairs on intramural needles and an additional electrode hook on the right atrium. Stimulus duration was 2 ms, and stimulus strength was just above threshold.

Preprocessing of the electrograms and tank ECG's consisted of gain adjusting based on calibration signals, establishing a linear baseline between adjacent T-P intervals, and windowing a representative beat. From a root mean squared curve of all signals, we manually set fiducial markers for QRS onset, QRS offset, and T-wave offset. To evaluate the accuracy of computed potentials in the torso volume with respect to measured data, we used relative error (RE), root mean squared error (RMS), and correlation coefficients (CC) as defined previously.[21] Results were presented as mean±standard deviation of signals at all compared locations.

Results

We first present comparison results between simulated potentials in the computer model and those measured with the torso tank preparation to validate the forward computation of volume and tank surface potentials. Then we computed currents and visualized potential and current distributions in the torso volume based on measurements on the heart surface under a variety of pacing conditions.

Validation of Computing Thoracic Potentials

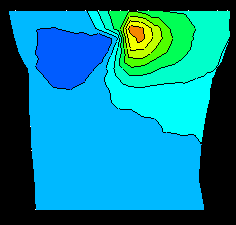
Figure 1 contains a comparison of measured potentials and those computed using the forward solution at 18 ms after QRS onset following right atrial (RA) pacing. Potentials on the torso surface, shown in both right-hand panels, exhibit a minimum in the midsternal region. This minimum is the surface manifestation of the right ventricular breakthrough (the arrival of excitation at the right ventricular surface), as indicated from potentials on a horizontal slice at the mid-ventricular level shown on the left panels. Computed potentials closely reconstruct these features, with matched locations of extrema on the torso surface, and similar patterns of potentials both in the volume and on the torso surface. The statistical comparison (shown in Table 1) between measured and computed potential maps at 1144 locations in the tank volume and surface over the 200 ms following QRS onset also shows good agreement. Correlation coefficients of 0.95 were obtained for both RA and left ventricular (LV) pacing. 0

Table 1: Comparison between measured and computed potentials

	RMS (mV)	RE	CC
RA pacing	0.07 ± 0.05	0.32 ± 0.11	0.95 ± 0.05
LV pacing	0.13 ± 0.09	0.30 ± 0.14	0.95 ± 0.07

**Figure 1:** Measured (upper panels) and computed potentials (lower panels) at 18 ms after QRS onset following right atrial pacing. Left-hand panels contain potentials on a horizontal cross section of the torso, and right-hand panels show potentials from the tank surface.

Thoracic Potentials and Currents

With the forward solution validated, we proceeded to compute thoracic currents and visualize these and the volume potentials under a variety of pacing conditions. Epicardial potentials exhibit a variety of patterns during different stages of the cardiac cycle and under different pacing sequences. We chose potential distributions with simple yet representative dipole or multiple dipole patterns, and computed thoracic potentials and currents. The following cases are examples selected specifically to illustrate relationships and features among epicardial potentials, thoracic potentials and currents, and body surface potentials.

Dipole Pattern During Atrial Pacing

At 8 ms after QRS onset following atrial pacing, epicardial potentials (Figure 2 Panel A) showed a well-defined dipole pattern, with positive potentials with the red shading covering the right side of the heart and negative potentials with the blue shading over the left side. This potential pattern coincided with septal excitation, which occurs in a predominantly left-to-right direction.[22] The potential maximum (1.9 mV) on the right ventricle and minimum (-2.1 mV) on the left ventricle served as current sources and sinks, respectively. In panel B, the red streamlines depict electrical current pathways in the volume conductor surrounding the heart. The streamlines represent current flow in the region defined by a set of seed points located just below the heart. In this case, current flow patterns near the heart resembled those of a current dipole field of approximately equal source and sink strength. The arrows in Panel B indicated the directions of currents flowing from the current sources to the current sinks.

Panel D of Figure 2 shows thoracic fields as both current streamlines and isosurfaces of potential (the dark green surface within the volume is the iso-potential surface at 0 mV). Features of thoracic electric fields visible in this figure include: (1) currents originated at the area of positive potential on the right ventricle and returned to the region of negative potential on the left ventricle; (2) some current loops were largely confined to the area close to the heart and did not result in potential gradients on the tank surface--the sources of such currents would not be directly visible in body surface potential measurements; and (3) current pathways determine potential distributions with each iso-potential surface always perpendicular to the current lines that pass through it (true for all isotropically conducting volume conductors). Panel C shows torso surface potentials from the same data, which also displayed a dipole pattern. Note that the zero-potential contour line on the torso surface (thick black line) is the intersection of the zero-potential isosurface in the torso volume (visible in Panel D) with the torso surface.

**Figure 2:** Electric fields at 8 ms after QRS onset during right atrial pacing. All four panels have the same perspective view from the front of the body. Panel A. Epicardial potentials: contour lines are equally distributed between -2.1 mV and 1.9 mV. Panel B. Current flow near the heart. Panel C. Body surface potentials: contour lines are drawn equally spaced between -1.16 mV and 0.66 mV. The thick black line is the iso-potential line at 0 mV. Panel D. Torso volume currents and potentials: streamlines depict current pathways, and the dark green surface within the volume is the iso-potential surface at 0 mV. The light green surface shows the posterior chest wall. The color shadings of potentials in the figure are similar to those in Figure 1, with red shading indicates potential maximum (plus sign) and blue shading indicates potential minimum (minus sign).

Single Ventricular Pacing Site

Figure 3 shows electric potentials and currents for a beat paced from a single site on the anterolateral surface of the left ventricle. In Panel A, epicardial potentials produced a well-defined pattern of a central minimum and dual maxima. The area of negativity (blue shading) covered the excited region in an elliptical shape. Near each end along the major axis of this elliptical region, there were two potential maxima (red shading with plus signs). The line joining the two potential maxima has shown to be an indication of local fiber direction.[23] Current pathways near the heart (Panel B) indicated two current loops, which started from two current sources at the potential maxima and merged into a single current path as they returned to the excited region of the heart (potential minimum).

In panel D, the multiple current loops near the heart emerged into a simpler pattern when flowing away the heart into the torso volume. The resulting pattern of current flow in the thorax (Panel D) shows currents flowing from the resting tissue of the heart indicated by positive potentials in the figure, and flowing into the excited tissue indicated by negative potentials. This current flow pattern is similar to the previous example when potentials on the heart surface had a simple dipole pattern. The dipole current flows resulted a zero-potential surface (the dark green surface within the volume) separating the torso volume into two regions. On the torso surface, only the current loop located anteriorly of the heart produced a dipole pattern with a strong negative pole (-4.6 mV) and a weak positive pole (0.39 mV). The other current loop started from the posterior potential maximum was too far away from the torso surface. Its currents emerged into the overall current flows in the torso and didn't produce visible manifestations in the tank surface potentials.

**Figure 3:** Electric field at 25 ms after an epicardial stimulus on the left ventricle. Same configuration as in Figure 2. Contour lines were drawn equally spaced between -6.28 mV and 0.95 mV on the epicardial surface and between -4.6 mV and 0.39 mV on the tank surface. The color shadings of potentials in the figure are similar to those in Figure 1, with red shading indicates potential maximum (plus sign) and blue shading indicates potential minimum (minus sign).

Multiple Ventricular Pacing Site

At 16 ms after simultaneous pacing at both the anterior and posterolateral surfaces of the left ventricle, epicardial potentials (Figure 4A) showed two distinct current sinks (regions of negative potential) at the pacing sites and distributed regions of positive potential. Potentials values at the anterior and posterolateral minima were -2.4 mV and -6.2 mV, respectively. Current loops near the heart produced two separate branches where flowing into the separate current sinks (Panel B).

In Panel D, surrounding the two current sinks, the dark green surfaces are iso-potential surfaces at -0.5 mV. The iso-surface around the anterior sink intersected the chest wall and contributed to the group of negative potential contour lines in the midsternal region (Panel C). By contrast, the iso-surface around the posterolateral sink did not reach the torso surface, and the same negativity (at -0.5 mV) did not appear on the tank surface. Even though the anterior potential minimum on the epicardial surface had a smaller magnitude than that of the posterolateral minimum (-2.4 mV vs. -6.2 mV), it produced a potential minimum on the tank surface eight times the magnitude of the one produced by the posterolateral minimum (-1.6 mV vs. -0.2 mV).

**Figure 4:** Electric fields at 16 ms after simultaneous pacing from two sites on the ventricular surface. Same configuration as in Figure 2. Contour lines were drawn equally spaced between -6.2 mV and 0.85 mV on the epicardial surface and between -1.6 mV and 0.38 mV on the tank surface. Potential values in mV were marked at the minima on both epicardial and tank surfaces (Panel A and C). The iso-potential surfaces in Panel C were at -0.5 mV.

Discussion

The goal of this study was to investigate the utility of visualizing three-dimensional electric potential and current fields generated by the heart. To this end, we have developed a simulation model to compute electric field in the torso volume and compared it to measurements in an isolated heart preparation. Simulated volume potentials closely matched measured potentials in the torso-tank preparation thus validating the general forward solution based approach we employed. Simulation further provided a means of estimating the current field in the torso from the computed torso volume potentials and the local geometric and conductive properties of the medium. We have developed and assembled a comprehensive numerical computation and visualization toolkit to explore current fields in the thorax. Applying these techniques to potentials measured from an isolated dog heart under a variety of pacing conditions, we have further demonstrated that thoracic current can provide many insights into the relationship between heart surface potential and body surface potentials. Specifically, we have shown that geometric factors including cardiac source configuration and location play an important role in determining to what extent electric activity in the heart is directly visible on the body surface electrocardiogram.

Our study based on the simplified conditions of the electrolytic torso tank suggested that geometric configuration can play key role in ECG measurements. In the example of simultaneous multiple pacing, two negative potential regions of similar strength on the cardiac surface showed very different influence on the tank surface simply due to their location relative to the volume conductor surrounding the heart. Clinical electrocardiographic events are often diagnosed based on the value of parameters extracted from the ECG, such as using ST deviation to detect ischemia and infarct. Many past studies[24,20] have recognized the importance of separating spatial factors from the underlying physiologic events. Visualizing thoracic potentials may provide a useful means to determine the nature of cardiac bioelectric sources and identify unique electrocardiographic features that as minimally influenced by geometric factors such as heart location and size.

Studying current field in the thorax provides additional insights from potential field into the role of the torso volume in determining body surface potentials. In the example of single pacing on the ventricular surface, the current flows near the heart had a complex pattern of multiple current loops. When currents flowed away from the heart into the torso volume, they emerged into current flows of a much simpler pattern due to the superposition property of the volume conductor. Accordingly, the body surface potentials showed a much simpler distributions than those on the heart surface.

The limitation of this study is our assumption of the torso volume as a homogeneous conducting medium. As we know, the torso is not homogeneous and possibly not isotropic. In a recent study[25], Klepfer et al. showed that inhomogeneous conductivity of different anatomical structures (subcutaneous fat, skeletal muscles, lungs, blood vessels, and bones) and anisotropy associated with skeletal muscles played an important role in the forward problem used to determine body surface potentials. Thus the results of our study will likely deviate from realistic conditions in the intact human torso. However, both simulation[6,25] and experimental studies[26] also showed that conducting properties of torso appeared to have only minor influence on the location of many key features of body surface potential but instead altered the shape and magnitude of these features. Hence, our conclusions regarding the effects of the geometry and cardiac source configuration on body surface potentials currents should be accurate in mechanism if not in every detail. The strongest motivation in developing the homogeneous torso model in this study was to take advantage of the validation ability provided by the (homogeneous) torso tank preparation. The finite element method we used in this study is well suited to incorporate inhomogeneity (including anisotropy) in the torso model, which is the topic of a future study in our laboratory.

The rationale for using currents instead of just electric potentials to describe cardiac fields lies in the nature of the fundamental bioelectric sources of these fields. During different phases of the cardiac cycle, membrane currents are the electric generators and sources of cardiac excitation and recovery. Electric currents induced by cardiac sources flow into the conducting medium in the thorax and determine potential fields in the thorax as well as potential distributions on the body surface. Thus, electric currents directly reflect physiologic events in the heart, and provide the fundamental connection between cardiac activity and the resulting body surface potentials. Whereas this study focused on exploring the extra-cardiac current field, the technical utilities for computing and visualizing current can also be extended to study intra-cardiac events. The ability to study current fields associated with excitation and recovery within the heart under both normal and pathophysiologic conditions, such as the ``injury current'' during ischemia, are likely to improve clinical interpretation of ECG.

Acknowledgments

We gratefully acknowledge Yonild Vyhmeister, Jayne Davis, Bob Lux, Phil Ershler, and Bruce Steadman at the CVRTI, for their assistance in the experiments. We thank David Weinstein at the Scientific Computing and Imaging Institute, University of Utah, for his assistance in using the SCIRun program. The support for this work comes from the University of Utah Graduate Research Fellowship (Quan Ni), the Whitaker Foundation, the Nora Eccles Treadwell Foundation and the Richard A. and Nora Eccles Harrison Fund for Cardiovascular Research.

Bibliography

1: M.S. Spach, R.C. Barr, C. Lanning, and P.C. Tucek.
Origin of body surface QRS and T wave potentials from epicardial potential distribution in the intact chimpanzee.
Circulation, 55:268-278, 1977.
2: M.S. Spach, R.C. Barr, and C. Lanning.
Experimental basis for QRS and T wave potentials in the WPW syndrome. the relation of epicardial to body surface potential distributions in the intact chimpanzee.
Circ Res, 42:103-118, 1978.
3: R.C. Barr, M. Ramsey, and M.S. Spach.
Relating epicardial to body surface potential distributions by means of transfer coefficients based on geometry measurements.
IEEE Trans Biomed Eng, 24(1):1-11, 1977.
4: Y. Rudy and R. Plonsey.
A comparison of volume conductor and source geometry on body surface and epicardial potentials.
Circ Res, 46(2):283-291, 1980.
5: H.S. Oster, B. Taccardi, R.L. Lux, P.R. Ershler, and Y. Rudy.
Noninvasive electrocardiographic imaging. reconstruction of epicardial potentials, electrograms, and isochrone and localization of single and multiple electrocardiac events.
Circulation, 96:1012-1024, 1997.
6: Y. Rudy and R. Plonsey.
The eccentric spheres model as the basis for a study of the role of geometry and inhomogeneities in electrocardiography.
IEEE Trans Biomed Eng, 26(7):392-399, 1979.
7: Y. Rudy, R. Plonsey, and J. Liebman.
The effects of variations in conductivity and geometrical parameters on the electrocardiogram, using an eccentric spheres model.
Circ Res, 44(1):104-111, 1979.
8: L. De Ambroggi and B. Taccardi.
Current and potential fields generated by two dipoles.
Circ. Res., 27:910-911, 1970.
9: P. Colli Franzone, L. Guerri, C. Viganotti, E. Macchi, S. Baruffi, S. Spaggiari, and B. Taccardi.
Potential fields generated by oblique dipole layers modeling excitation wavefronts in the anisotropic myocardium.
Circ Res, 51:330-346, 1982.
10: C.R. Johnson and R.S. MacLeod.
Computer models for calculating transthoracic current flow.
In Proceedings of the IEEE Engineering in Medicine and Biology Society 13th Annual International Conference, pages 768-769. IEEE Press, 1991.
11: C.R. Johnson, R.S. MacLeod, and P.R. Ershler.
A computer model for the study of electrical current flow in the human thorax.
Comp. in Biol. & Med., 22:305-323, 1992.
12: C.R. Johnson, R.S. MacLeod, and M.A. Matheson.
Computer simulations reveal complexity of electrical activity in the human thorax.
Computers in Physics., 6(3):230-237, 1992.
13: C.R. Johnson.
Computational and numerical methods for bioelectric field problems.
CRC Crit Rev Biomed Eng, 25:1-81, 1997.
14: Q. Ni, R.S. MacLeod, and R.L. Lux.
Three-dimensional activation mapping in ventricular muscles: Interpolation and approximation of activation times.
Annals of Biomedical Engineering, 27(5):617-626, 1999.
15: W. Schroeder, K. Martin, and B. Lorensen.
The Visualization Toolkit: An Object-oriented Approach to 3D Graphics.
Prentice Hall PTR, 2nd edition, 1996.
16: S.G. Parker, D.W. Weinstein, and C.R. Johnson.
The scirun computational steering software system.
In E. Arge, A.M. Bruaset, and H.P. Langtangen, editors, Modern software tools in scientific computing, pages 1-40. Birkhauser Press, 1997.
17: R.S. MacLeod, C.R. Johnson, and M.A. Matheson.
Visualization of cardiac bioelectricity -- a case study.
In Proceedings of the IEEE Visualization 92, pages 411-418. IEEE CS Press, 1992.
18: R.S. MacLeod, C.R. Johnson, and M.A. Matheson.
Visualizing bioelectric fields.
IEEE Comp. Graph. & Applic., 13(4):10-12, 1993.
19: R.S. MacLeod, R.L. Lux, M.S. Fuller, and B. Taccardi.
Evaluation of novel measurement methods for detecting heterogeneous repolarization.
J Electrocardiol, 29 Suppl.:145-153, 1996.
20: R.S. MacLeod, R.L. Lux, and B. Taccardi.
A possible mechanism for electrocardiographically silent changes in cardiac repolarization.
J Electrocardiol, 30(Supple):114-121, 1997.
21: Q. Ni, R.S. MacLeod, R.L. Lux, and B. Taccardi.
A novel interpolation method for electric potential fields in the heart during excitation.
Annals Biomed Engineering, 26(4):597-607, 1998.
22: Dirk Durrer, R.Th. van Dam, G.E. Freud, M.J. Janse, F.L. Meijler, and R.C. Arzbaecher.
Total excitation of the isolated human heart.
Circulation, 41:899-912, 1970.
23: B. Taccardi, E. Macchi, R.L. Lux, P.R. Ershler, S. Spaggiari, S. Baruffi, and Y. Vyhmeister.
Effect of myocardial fiber direction on epicardial potentials.
Circulation, 90:3076-3090, 1994.
24: R.P. Holland and H. Brooks.
TQ-ST segment mapping: critical review and analysis of current concepts.
Am J Cardiol, 40:110-129, 1977.
25: R.N. Klepfer, C.R. Johnson, and R.S. MacLeod.
The effects of inhomogeneities and anisotropies on electrocardiographic fields: A three-dimensional finite element study.
IEEE Trans Biomed Eng, 44(8):706-719, 1997.
26: L.S. Green, B. Taccardi, P.R. Ershler, and R.L. Lux.
Epicardial potential mapping: Effects of conducting media on isopotential and isochrone distributions.
Circulation, 84:2513-2521, 1991.

Tables and Figures

Table: Comparison between measured and computed potentials

	RMS (mV)	RE	CC
RA pacing	0.07 ± 0.05	0.32 ± 0.11	0.95 ± 0.05
LV pacing	0.13 ± 0.09	0.30 ± 0.14	0.95 ± 0.07

**Figure:** Measured (upper panels) and computed potentials (lower panels) at 18 ms after QRS onset following right atrial pacing. Left-hand panels contain potentials on a horizontal cross section of the torso, and right-hand panels show potentials from the tank surface.

**Figure:** Electric fields at 8 ms after QRS onset during right atrial pacing. All four panels have the same perspective view from the front of the body. Panel A. Epicardial potentials: contour lines are equally distributed between -2.1 mV and 1.9 mV. Panel B. Current flow near the heart. Panel C. Body surface potentials: contour lines are drawn equally spaced between -1.16 mV and 0.66 mV. The thick black line is the iso-potential line at 0 mV. Panel D. Torso volume currents and potentials: streamlines depict current pathways, and the dark green surface within the volume is the iso-potential surface at 0 mV. The light green surface shows the posterior chest wall. The color shadings of potentials in the figure are similar to those in Figure 1, with red shading indicates potential maximum (plus sign) and blue shading indicates potential minimum (minus sign).

**Figure:** Electric field at 25 ms after an epicardial stimulus on the left ventricle. Same configuration as in Figure 2. Contour lines were drawn equally spaced between -6.28 mV and 0.95 mV on the epicardial surface and between -4.6 mV and 0.39 mV on the tank surface. The color shadings of potentials in the figure are similar to those in Figure 1, with red shading indicates potential maximum (plus sign) and blue shading indicates potential minimum (minus sign).

**Figure:** Electric fields at 16 ms after simultaneous pacing from two sites on the ventricular surface. Same configuration as in Figure 2. Contour lines were drawn equally spaced between -6.2 mV and 0.85 mV on the epicardial surface and between -1.6 mV and 0.38 mV on the tank surface. Potential values in mV were marked at the minima on both epicardial and tank surfaces (Panel A and C). The iso-potential surfaces in Panel C were at -0.5 mV.

About this document ...

Computing and Visualizing Electric Potentials and Current Pathways in the Thorax

This document was generated using the LaTeX2HTML translator Version 99.2beta6 (1.42)

The command line arguments were:
latex2html -split 3 -no_white -link 3 -no_navigation -nomath -html_version 3.2,math paper

The translation was initiated by Rob MacLeod on 2000-11-09

Rob MacLeod 2000-11-09