Scientific Computing
Numerical simulation of real-world phenomena provides fertile ground for building interdisciplinary relationships. The SCI Institute has a long tradition of building these relationships in a win-win fashion – a win for the theoretical and algorithmic development of numerical modeling and simulation techniques and a win for the discipline-specific science of interest. High-order and adaptive methods, uncertainty quantification, complexity analysis, and parallelization are just some of the topics being investigated by SCI faculty. These areas of computing are being applied to a wide variety of engineering applications ranging from fluid mechanics and solid mechanics to bioelectricity.
Valerio Pascucci
Scientific Data Management
Chris Johnson
Problem Solving Environments
Ross Whitaker
GPUs
Chuck Hansen
GPUsFunded Research Projects:
Publications in Scientific Computing:
  Adaptive High-Order Discontinuous Galerkin Solution of Elastohydrodynamic Lubrication Point Contact Problems H. Lu, M. Berzins, C.E. Goodyer, P.K. Jimack. In Advances in Engineering Software, Vol. 45, No. 1, pp. 313--324. 2012. DOI: 10.1016/j.advengsoft.2011.10.006 This paper describes an adaptive implementation of a high order Discontinuous Galerkin (DG) method for the solution of elastohydrodynamic lubrication (EHL) point contact problems. These problems arise when modelling the thin lubricating film between contacts which are under sufficiently high pressure that the elastic deformation of the contacting elements cannot be neglected. The governing equations are highly nonlinear and include a second order partial differential equation that is derived via the thin-film approximation. Furthermore, the problem features a free boundary, which models where cavitation occurs, and this is automatically captured as part of the solution process. The need for spatial adaptivity stems from the highly variable length scales that are present in typical solutions. Results are presented which demonstrate both the effectiveness and the limitations of the proposed adaptive algorithm. Keywords: Elastohydrodynamic lubrication, Discontinuous Galerkin, High polynomial degree, h-adaptivity, Nonlinear systems |
  An optimization framework for inversely estimating myocardial transmembrane potentials and localizing ischemia D. Wang, R.M. Kirby, R.S. Macleod, C.R. Johnson. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS), pp. 1680--1683. 2011. DOI: 10.1109/IEMBS.2011.6090483 PubMed ID: 22254648 PubMed Central ID: PMC3336368 By combining a static bidomain heart model with a torso conduction model, we studied the inverse electrocardiographic problem of computing the transmembrane potentials (TMPs) throughout the myocardium from a body-surface potential map, and then used the recovered potentials to localize myocardial ischemia. Our main contribution is solving the inverse problem within a constrained optimization framework, which is a generalization of previous methods for calculating transmembrane potentials. The framework offers ample flexibility for users to apply various physiologically-based constraints, and is well supported by mature algorithms and solvers developed by the optimization community. By avoiding the traditional inverse ECG approach of building the lead-field matrix, the framework greatly reduces computation cost and, by setting the associated forward problem as a constraint, the framework enables one to flexibly set individualized resolutions for each physical variable, a desirable feature for balancing model accuracy, ill-conditioning and computation tractability. Although the task of computing myocardial TMPs at an arbitrary time instance remains an open problem, we showed that it is possible to obtain TMPs with moderate accuracy during the ST segment by assuming all cardiac cells are at the plateau phase. Moreover, the calculated TMPs yielded a good estimate of ischemic regions, which was of more clinical interest than the voltage values themselves. We conducted finite element simulations of a phantom experiment over a 2D torso model with synthetic ischemic data. Preliminary results indicated that our approach is feasible and suitably accurate for the common case of transmural myocardial ischemia. |
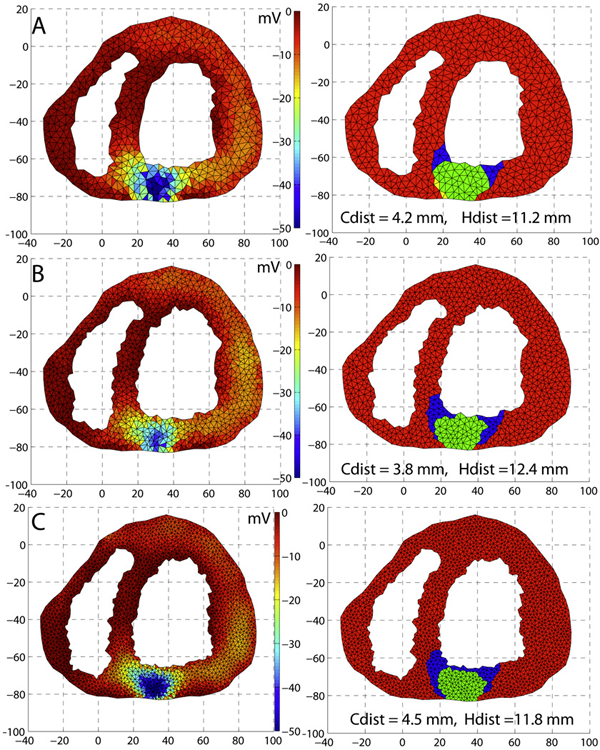
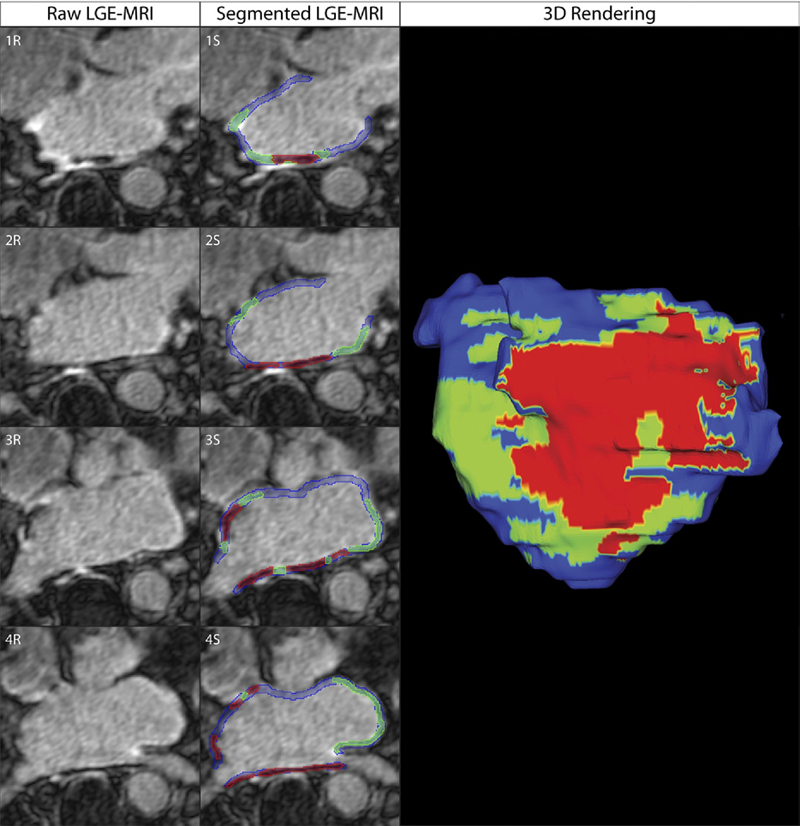
  Dark Regions of No-Reflow on Late Gadolinium Enhancement Magnetic Resonance Imaging Result in Scar Formation After Atrial Fibrillation Ablation C.J. McGann, E.G. Kholmovski, J.J. Blauer, S. Vijayakumar, T.S. Haslam, J.E. Cates, E.V. DiBella, N.S. Burgon, B. Wilson, A.J. Alexander, M.W. Prastawa, M. Daccarett, G. Vergara, N.W. Akoum, D.L. Parker, R.S. MacLeod, N.F. Marrouche. In Journal of the American College of Cardiology, Vol. 58, No. 2, pp. 177--185. 2011. DOI: 10.1016/j.jacc.2011.04.008 PubMed ID: 21718914 Objectives: The aim of this study was to assess acute ablation injuries seen on late gadolinium enhancement (LGE) magnetic resonance imaging (MRI) immediately post-ablation (IPA) and the association with permanent scar 3 months post-ablation (3moPA). Background: Success rates for atrial fibrillation catheter ablation vary significantly, in part because of limited information about the location, extent, and permanence of ablation injury at the time of procedure. Although the amount of scar on LGE MRI months after ablation correlates with procedure outcomes, early imaging predictors of scar remain elusive. Methods: Thirty-seven patients presenting for atrial fibrillation ablation underwent high-resolution MRI with a 3-dimensional LGE sequence before ablation, IPA, and 3moPA using a 3-T scanner. The acute left atrial wall injuries on IPA scans were categorized as hyperenhancing (HE) or nonenhancing (NE) and compared with scar 3moPA. Results: Heterogeneous injuries with HE and NE regions were identified in all patients. Dark NE regions in the left atrial wall on LGE MRI demonstrate findings similar to the \"no-reflow\" phenomenon. Although the left atrial wall showed similar amounts of HE, NE, and normal tissue IPA (37.7 ± 13\%, 34.3 ± 14\%, and 28.0 ± 11\%, respectively; p = NS), registration of IPA injuries with 3moPA scarring demonstrated that 59.0 ± 19\% of scar resulted from NE tissue, 30.6 ± 15\% from HE tissue, and 10.4 ± 5\% from tissue identified as normal. Paired t-test comparisons were all statistically significant among NE, HE, and normal tissue types (p less than 0.001). Arrhythmia recurrence at 1-year follow-up correlated with the degree of wall enhancement 3moPA (p = 0.02). Conclusion: Radiofrequency ablation results in heterogeneous injury on LGE MRI with both HE and NE wall lesions. The NE lesions demonstrate no-reflow characteristics and reveal a better predictor of final scar at 3 months. Scar correlates with procedure outcomes, further highlighting the importance of early scar prediction. (J Am Coll Cardiol 2011;58:177–85) © 2011 by the American College of Cardiology Foundation |
  Efficient Implementation of Smoothness-Increasing Accuracy-Conserving (SIAC) Filters for Discontinuous Galerkin Solutions H. Mirzaee, J.K. Ryan, R.M. Kirby. In Journal of Scientific Computing, pp. (in press). 2011. DOI: 10.1007/s10915-011-9535-x The discontinuous Galerkin (DG) methods provide a high-order extension of the finite volume method in much the same way as high-order or spectral/hp elements extend standard finite elements. However, lack of inter-element continuity is often contrary to the smoothness assumptions upon which many post-processing algorithms such as those used in visualization are based. Smoothness-increasing accuracy-conserving (SIAC) filters were proposed as a means of ameliorating the challenges introduced by the lack of regularity at element interfaces by eliminating the discontinuity between elements in a way that is consistent with the DG methodology; in particular, high-order accuracy is preserved and in many cases increased. The goal of this paper is to explicitly define the steps to efficient computation of this filtering technique as applied to both structured triangular and quadrilateral meshes. Furthermore, as the SIAC filter is a good candidate for parallelization, we provide, for the first time, results that confirm anticipated performance scaling when parallelized on a shared-memory multi-processor machine. |
  To CG or to HDG: A Comparative Study R.M. Kirby, B. Cockburn, S.J. Sherwin. In Journal of Scientific Computing, Note: published online, 2011. DOI: 10.1007/s10915-011-9501-7 Hybridization through the border of the elements (hybrid unknowns) combined with a Schur complement procedure (often called static condensation in the context of continuous Galerkin linear elasticity computations) has in various forms been advocated in the mathematical and engineering literature as a means of accomplishing domain decomposition, of obtaining increased accuracy and convergence results, and of algorithm optimization. Recent work on the hybridization of mixed methods, and in particular of the discontinuous Galerkin (DG) method, holds the promise of capitalizing on the three aforementioned properties; in particular, of generating a numerical scheme that is discontinuous in both the primary and flux variables, is locally conservative, and is computationally competitive with traditional continuous Galerkin (CG) approaches. In this paper we present both implementation and optimization strategies for the Hybridizable Discontinuous Galerkin (HDG) method applied to two dimensional elliptic operators. We implement our HDG approach within a spectral/hp element framework so that comparisons can be done between HDG and the traditional CG approach. We demonstrate that the HDG approach generates a global trace space system for the unknown that although larger in rank than the traditional static condensation system in CG, has significantly smaller bandwidth at moderate polynomial orders. We show that if one ignores set-up costs, above approximately fourth-degree polynomial expansions on triangles and quadrilaterals the HDG method can be made to be as efficient as the CG approach, making it competitive for time-dependent problems even before taking into consideration other properties of DG schemes such as their superconvergence properties and their ability to handle hp-adaptivity. |
  Formal Specification of MPI 2.0: Case Study in Specifying a Practical Concurrent Programming API G. Li, R. Palmer, M. DeLisi, G. Gopalakrishnan, R.M. Kirby. In Science of Computer Programming, Vol. 76, pp. 65--81. 2011. DOI: 10.1016/j.scico.2010.03.007 We describe the first formal specification of a non-trivial subset of MPI, the dominant communication API in high performance computing. Engineering a formal specification for a non-trivial concurrency API requires the right combination of rigor, executability, and traceability, while also serving as a smooth elaboration of a pre-existing informal specification. It also requires the modularization of reusable specification components to keep the length of the specification in check. Long-lived APIs such as MPI are not usually 'textbook minimalistic' because they support a diverse array of applications, a diverse community of users, and have efficient implementations over decades of computing hardware. We choose the TLA+ notation to write our specifications, and describe how we organized the specification of around 200 of the 300 MPI 2.0 functions. We detail a handful of these functions in this paper, and assess our specification with respect to the aforementioned requirements. We close with a description of possible approaches that may help render the act of writing, understanding, and validating the specifications of concurrency APIs much more productive. |
  Direct Isosurface Visualization of Hex-Based High-Order Geometry and Attribute Representations T. Martin, E. Cohen, R.M. Kirby. In IEEE Transactions on Visualization and Computer Graphics (TVCG), Vol. PP, No. 99, pp. 1--14. 2011. ISSN: 1077-2626 DOI: 10.1109/TVCG.2011.103 In this paper, we present a novel isosurface visualization technique that guarantees the accuarate visualization of isosurfaces with complex attribute data defined on (un-)structured (curvi-)linear hexahedral grids. Isosurfaces of high-order hexahedralbased finite element solutions on both uniform grids (including MRI and CT scans) and more complex geometry represent a domain of interest that can be rendered using our algorithm. Additionally, our technique can be used to directly visualize solutions and attributes in isogeometric analysis, an area based on trivariate high-order NURBS (Non-Uniform Rational B-splines) geometry and attribute representations for the analysis. Furthermore, our technique can be used to visualize isosurfaces of algebraic functions. Our approach combines subdivision and numerical root-finding to form a robust and efficient isosurface visualization algorithm that does not miss surface features, while finding all intersections between a view frustum and desired isosurfaces. This allows the use of view-independent transparency in the rendering process. We demonstrate our technique through a straightforward CPU implementation on both complexstructured and complex-unstructured geometry with high-order simulation solutions, isosurfaces of medical data sets, and isosurfaces of algebraic functions. |
  Finite element implementation of mechanochemical phenomena in neutral deformable porous media under finite deformation G.A. Ateshian, M.B. Albro, S.A. Maas, J.A. Weiss. In Journal of Biomechanical Engineering, Vol. 133, No. 8, 2011. DOI: 10.1115/1.4004810 Biological soft tissues and cells may be subjected to mechanical as well as chemical (osmotic) loading under their natural physiological environment or various experimental conditions. The interaction of mechanical and chemical effects may be very significant under some of these conditions, yet the highly nonlinear nature of the set of governing equations describing these mechanisms poses a challenge for the modeling of such phenomena. This study formulated and implemented a finite element algorithm for analyzing mechanochemical events in neutral deformable porous media under finite deformation. The algorithm employed the framework of mixture theory to model the porous permeable solid matrix and interstitial fluid, where the fluid consists of a mixture of solvent and solute. A special emphasis was placed on solute-solid matrix interactions, such as solute exclusion from a fraction of the matrix pore space (solubility) and frictional momentum exchange that produces solute hindrance and pumping under certain dynamic loading conditions. The finite element formulation implemented full coupling of mechanical and chemical effects, providing a framework where material properties and response functions may depend on solid matrix strain as well as solute concentration. The implementation was validated using selected canonical problems for which analytical or alternative numerical solutions exist. This finite element code includes a number of unique features that enhance the modeling of mechanochemical phenomena in biological tissues. The code is available in the public domain, open source finite element program FEBio (http://mrl.sci.utah.edu/software). [DOI: 10.1115/1.4004810] |
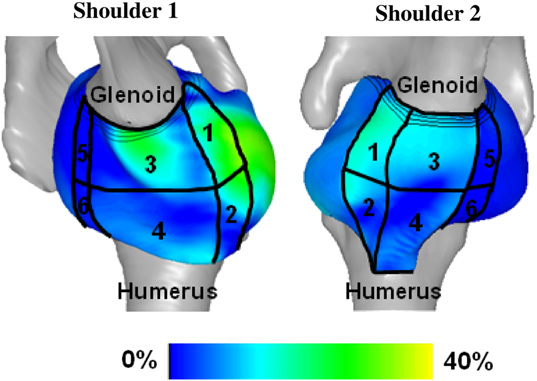
  Finding consistent strain distributions in the glenohumeral capsule between two subjects: Implications for development of physical examinations N.J. Drury, B.J. Ellis, J.A. Weiss, P.J. McMahon, R.E. Debski. In Journal of Biomechanics, Vol. 44, No. 4, pp. 607-613. February, 2011. DOI: 10.1016/j.jbiomech.2010.11.018 The anterior-inferior glenohumeral capsule is the primary passive stabilizer to the glenohumeral joint during anterior dislocation. Physical examinations following dislocation are crucial for proper diagnosis of capsule pathology; however,they are not standardized for joint position which may lead to misdiagnoses and poor outcomes. To suggest joint positions for physical examinations where the stability provided by the capsule may be consistent among patients, the objective of this study was to evaluate the distribution of maximum principal strain on the anterior-inferior capsule using two validated subject-specific finite element models of the glenohumeral joint at clinically relevant joint positions. The joint positions with 25 N anterior load applied at 60° of glenohumeral abduction and 10°, 20°, 30° and 40° of external rotation resulted in distributions of strain that were similar between shoulders(r2≥0.7). Furthermore, those positions with 20-40° of external rotation resulted in capsule strains on the glenoid side of the anterior band of the inferior glenohumeral ligament that were significantly greater than in all other capsule regions. These findings suggest that anterior stability provided by the anterior-inferior capsule may be consistent among subjects at joint positions with 60° of glenohumeral abduction and a mid-range (20-40°) of external rotation, and that the glenoid side has the greatest contribution to stability at these joint positions. Therefore, it may be possible to establish standard joint positions for physical examinations that clinicians can use to effectively diagnose pathology in the anterior-inferior capsule following dislocation and lead to improved outcomes. |
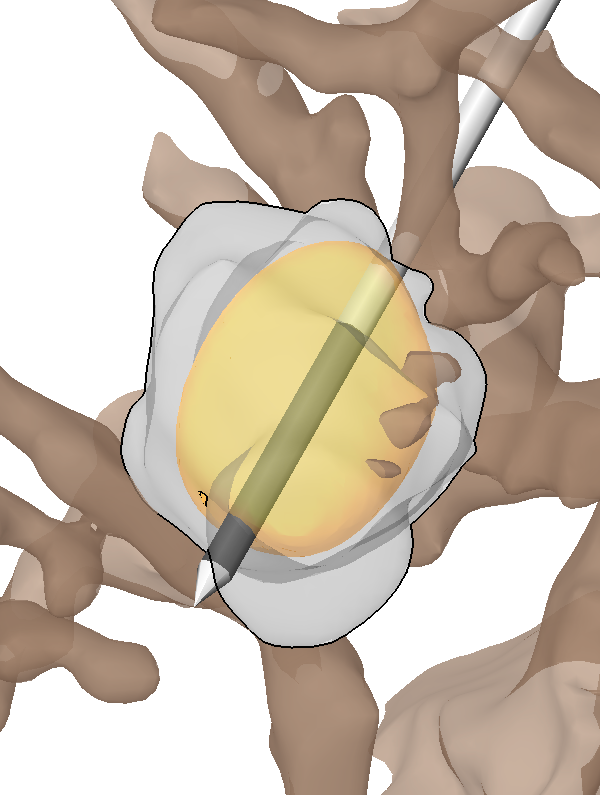
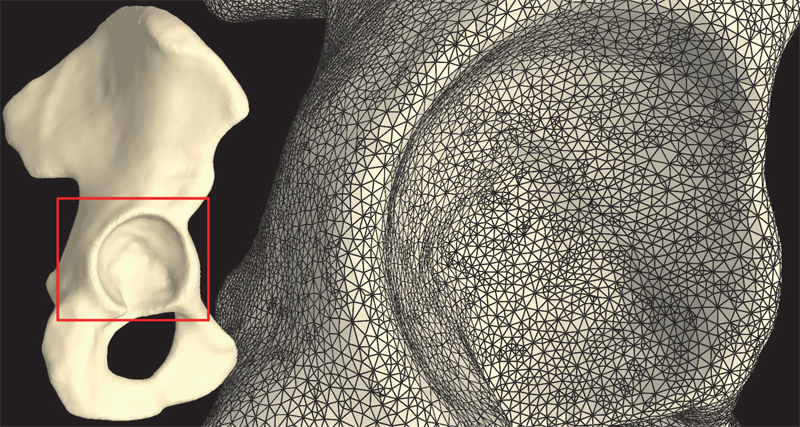
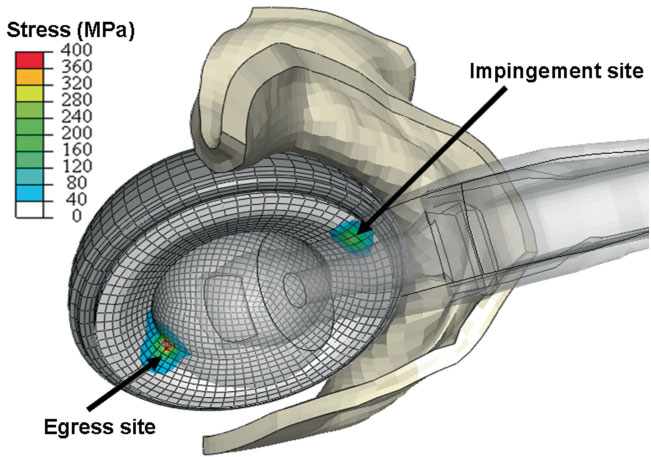
  The capsule's contribution to total hip construct stability - a finite element analysis J.M. Elkins, J.S. Stroud, M.J. Rudert, Y. Tochigi, D.R. Pedersen, B.J. Ellis, J.J. Callaghan, J.A. Weiss, T.D. Brown. In Journal of Orthopedic Research, Vol. 29, No. 11, Note: William Harris, MD Award, pp. 1642--1648. November, 2011. DOI: 10.1002/jor.21435 Instability is a significant concern in total hip arthroplasty (THA), particularly when there is structural compromise of the capsule due to pre-existing pathology or due to necessities of surgical approach. An experimentally grounded fiber-direction-based finite element model of the hip capsule was developed, and was integrated with an established three-dimensional model of impingement/dislocation. Model validity was established by close similarity to results from a cadaveric experiment in a servohydraulic hip simulator. Parametric computational runs explored effects of graded levels of capsule thickness, of regional detachment from the capsule's femoral or acetabular insertions, of surgical incisions of capsule substance, and of capsule defect repairs. Depending strongly upon the specific site, localized capsule defects caused varying degrees of construct stability compromise, with several specific situations involving over 60\% decrement in dislocation resistance. Construct stability was returned substantially toward intact-capsule levels following well-conceived repairs, although the suture sites involved were often at substantial risk of failure. These parametric model results underscore the importance of retaining or robustly repairing capsular structures in THA, in order to maximize overall construct stability. © 2011 Orthopaedic Research Society. Published by Wiley Periodicals, Inc. J Orthop Res 29:1642–1648, 2011 |