SCI Publications
2011
C.D. Cantwell, S.J. Sherwin, R.M. Kirby, P.H.J. Kelly.
“From h to p Efficiently: Selecting the Optimal Spectral/hp Discretisation in Three Dimensions,” In Mathematical Modelling of Natural Phenomena, Vol. 6, No. 3, pp. 84--96. 2011.
T. Etiene, L.G. Nonato, C. Scheidegger, J. Tierny, T.J. Peters, V. Pascucci, R.M. Kirby, C.T. Silva.
“Topology Verfication for Isosurface Extraction,” In IEEE Transactions on Visualization and Computer Graphics, pp. (accepted). 2011.

Z. Fu, W.-K. Jeong, Y. Pan, R.M. Kirby, R.T. Whitaker.
“A fast iterative method for solving the Eikonal equation on triangulated surfaces,” In SIAM Journal of Scientific Computing, Vol. 33, No. 5, pp. 2468--2488. 2011.
DOI: 10.1137/100788951
PubMed Central ID: PMC3360588
This paper presents an efficient, fine-grained parallel algorithm for solving the Eikonal equation on triangular meshes. The Eikonal equation, and the broader class of Hamilton–Jacobi equations to which it belongs, have a wide range of applications from geometric optics and seismology to biological modeling and analysis of geometry and images. The ability to solve such equations accurately and efficiently provides new capabilities for exploring and visualizing parameter spaces and for solving inverse problems that rely on such equations in the forward model. Efficient solvers on state-of-the-art, parallel architectures require new algorithms that are not, in many cases, optimal, but are better suited to synchronous updates of the solution. In previous work [W. K. Jeong and R. T. Whitaker, SIAM J. Sci. Comput., 30 (2008), pp. 2512–2534], the authors proposed the fast iterative method (FIM) to efficiently solve the Eikonal equation on regular grids. In this paper we extend the fast iterative method to solve Eikonal equations efficiently on triangulated domains on the CPU and on parallel architectures, including graphics processors. We propose a new local update scheme that provides solutions of first-order accuracy for both architectures. We also propose a novel triangle-based update scheme and its corresponding data structure for efficient irregular data mapping to parallel single-instruction multiple-data (SIMD) processors. We provide detailed descriptions of the implementations on a single CPU, a multicore CPU with shared memory, and SIMD architectures with comparative results against state-of-the-art Eikonal solvers.
S.E. Geneser, J.D. Hinkle, R.M. Kirby, Bo Wang, B. Salter, S. Joshi.
“Quantifying variability in radiation dose due to respiratory-induced tumor motion,” In Medical Image Analysis, Vol. 15, No. 4, pp. 640--649. 2011.
DOI: 10.1016/j.media.2010.07.003
G. Gopalakrishnan, R.M. Kirby, S. Siegel, R. Thakur, W. Gropp, E. Lusk, B.R. de Supinski, M. Schultz, G. Bronevetsky.
“Formal Analysis of MPI-Based Parallel Programs: Present and Future,” In Communications of the ACM, pp. (accepted). 2011.
S.A. Isaacson, R.M. Kirby.
“Numerical Solution of Linear Volterra Integral Equations of the Second Kind with Sharp Gradients,” In Journal of Computational and Applied Mathematics, Vol. 235, No. 14, pp. 4283--4301. 2011.
Collocation methods are a well-developed approach for the numerical solution of smooth and weakly singular Volterra integral equations. In this paper, we extend these methods through the use of partitioned quadrature based on the qualocation framework, to allow the efficient numerical solution of linear, scalar Volterra integral equations of the second kind with smooth kernels containing sharp gradients. In this case, the standard collocation methods may lose computational efficiency despite the smoothness of the kernel. We illustrate how the qualocation framework can allow one to focus computational effort where necessary through improved quadrature approximations, while keeping the solution approximation fixed. The computational performance improvement introduced by our new method is examined through several test examples. The final example we consider is the original problem that motivated this work: the problem of calculating the probability density associated with a continuous-time random walk in three dimensions that may be killed at a fixed lattice site. To demonstrate how separating the solution approximation from quadrature approximation may improve computational performance, we also compare our new method to several existing Gregory, Sinc, and global spectral methods, where quadrature approximation and solution approximation are coupled.
P.K. Jimack, R.M. Kirby.
“Towards the Development on an h-p-Refinement Strategy Based Upon Error Estimate Sensitivity,” In Computers and Fluids, Vol. 46, No. 1, pp. 277--281. 2011.
The use of (a posteriori) error estimates is a fundamental tool in the application of adaptive numerical methods across a range of fluid flow problems. Such estimates are incomplete however, in that they do not necessarily indicate where to refine in order to achieve the most impact on the error, nor what type of refinement (for example h-refinement or p-refinement) will be best. This paper extends preliminary work of the authors (Comm Comp Phys, 2010;7:631–8), which uses adjoint-based sensitivity estimates in order to address these questions, to include application with p-refinement to arbitrary order and the use of practical a posteriori estimates. Results are presented which demonstrate that the proposed approach can guide both the h-refinement and the p-refinement processes, to yield improvements in the adaptive strategy compared to the use of more orthodox criteria.
R.M. Kirby, B. Cockburn, S.J. Sherwin.
“To CG or to HDG: A Comparative Study,” In Journal of Scientific Computing, Note: published online, 2011.
DOI: 10.1007/s10915-011-9501-7
Hybridization through the border of the elements (hybrid unknowns) combined with a Schur complement procedure (often called static condensation in the context of continuous Galerkin linear elasticity computations) has in various forms been advocated in the mathematical and engineering literature as a means of accomplishing domain decomposition, of obtaining increased accuracy and convergence results, and of algorithm optimization. Recent work on the hybridization of mixed methods, and in particular of the discontinuous Galerkin (DG) method, holds the promise of capitalizing on the three aforementioned properties; in particular, of generating a numerical scheme that is discontinuous in both the primary and flux variables, is locally conservative, and is computationally competitive with traditional continuous Galerkin (CG) approaches. In this paper we present both implementation and optimization strategies for the Hybridizable Discontinuous Galerkin (HDG) method applied to two dimensional elliptic operators. We implement our HDG approach within a spectral/hp element framework so that comparisons can be done between HDG and the traditional CG approach.
We demonstrate that the HDG approach generates a global trace space system for the unknown that although larger in rank than the traditional static condensation system in CG, has significantly smaller bandwidth at moderate polynomial orders. We show that if one ignores set-up costs, above approximately fourth-degree polynomial expansions on triangles and quadrilaterals the HDG method can be made to be as efficient as the CG approach, making it competitive for time-dependent problems even before taking into consideration other properties of DG schemes such as their superconvergence properties and their ability to handle hp-adaptivity.
G. Li, R. Palmer, M. DeLisi, G. Gopalakrishnan, R.M. Kirby.
“Formal Specification of MPI 2.0: Case Study in Specifying a Practical Concurrent Programming API,” In Science of Computer Programming, Vol. 76, pp. 65--81. 2011.
DOI: 10.1016/j.scico.2010.03.007
We describe the first formal specification of a non-trivial subset of MPI, the dominant communication API in high performance computing. Engineering a formal specification for a non-trivial concurrency API requires the right combination of rigor, executability, and traceability, while also serving as a smooth elaboration of a pre-existing informal specification. It also requires the modularization of reusable specification components to keep the length of the specification in check. Long-lived APIs such as MPI are not usually 'textbook minimalistic' because they support a diverse array of applications, a diverse community of users, and have efficient implementations over decades of computing hardware. We choose the TLA+ notation to write our specifications, and describe how we organized the specification of around 200 of the 300 MPI 2.0 functions. We detail a handful of these functions in this paper, and assess our specification with respect to the aforementioned requirements. We close with a description of possible approaches that may help render the act of writing, understanding, and validating the specifications of concurrency APIs much more productive.
T. Martin, E. Cohen, R.M. Kirby.
“Direct Isosurface Visualization of Hex-Based High-Order Geometry and Attribute Representations,” In IEEE Transactions on Visualization and Computer Graphics (TVCG), Vol. PP, No. 99, pp. 1--14. 2011.
ISSN: 1077-2626
DOI: 10.1109/TVCG.2011.103
In this paper, we present a novel isosurface visualization technique that guarantees the accuarate visualization of isosurfaces with complex attribute data defined on (un-)structured (curvi-)linear hexahedral grids. Isosurfaces of high-order hexahedralbased finite element solutions on both uniform grids (including MRI and CT scans) and more complex geometry represent a domain of interest that can be rendered using our algorithm. Additionally, our technique can be used to directly visualize solutions and attributes in isogeometric analysis, an area based on trivariate high-order NURBS (Non-Uniform Rational B-splines) geometry and attribute representations for the analysis. Furthermore, our technique can be used to visualize isosurfaces of algebraic functions. Our approach combines subdivision and numerical root-finding to form a robust and efficient isosurface visualization algorithm that does not miss surface features, while finding all intersections between a view frustum and desired isosurfaces. This allows the use of view-independent transparency in the rendering process. We demonstrate our technique through a straightforward CPU implementation on both complexstructured and complex-unstructured geometry with high-order simulation solutions, isosurfaces of medical data sets, and isosurfaces of algebraic functions.
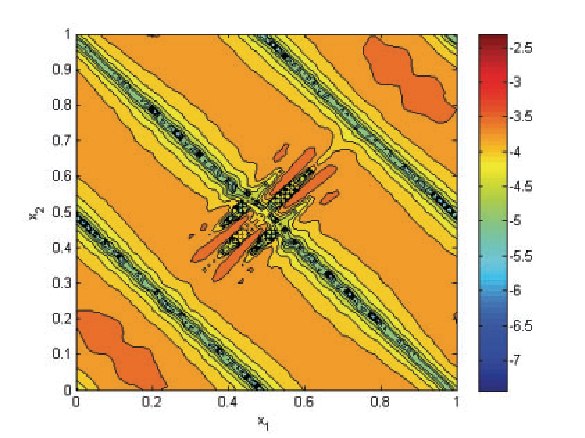
H. Mirzaee, Liangyue, J.K. Ryan, R.M. Kirby.
“Smoothness-Increasing Accuracy-Conserving (SIAC) Postprocessing for Discontinuous Galerkin Solutions Over Structured Triangular Meshes,” In SIAM Journal of Numerical Analysis, Vol. 49, No. 5, pp. 1899--1920. 2011.
H. Mirzaee, J.K. Ryan, R.M. Kirby.
“Efficient Implementation of Smoothness-Increasing Accuracy-Conserving (SIAC) Filters for Discontinuous Galerkin Solutions,” In Journal of Scientific Computing, pp. (in press). 2011.
DOI: 10.1007/s10915-011-9535-x
The discontinuous Galerkin (DG) methods provide a high-order extension of the finite volume method in much the same way as high-order or spectral/hp elements extend standard finite elements. However, lack of inter-element continuity is often contrary to the smoothness assumptions upon which many post-processing algorithms such as those used in visualization are based. Smoothness-increasing accuracy-conserving (SIAC) filters were proposed as a means of ameliorating the challenges introduced by the lack of regularity at element interfaces by eliminating the discontinuity between elements in a way that is consistent with the DG methodology; in particular, high-order accuracy is preserved and in many cases increased. The goal of this paper is to explicitly define the steps to efficient computation of this filtering technique as applied to both structured triangular and quadrilateral meshes. Furthermore, as the SIAC filter is a good candidate for parallelization, we provide, for the first time, results that confirm anticipated performance scaling when parallelized on a shared-memory multi-processor machine.
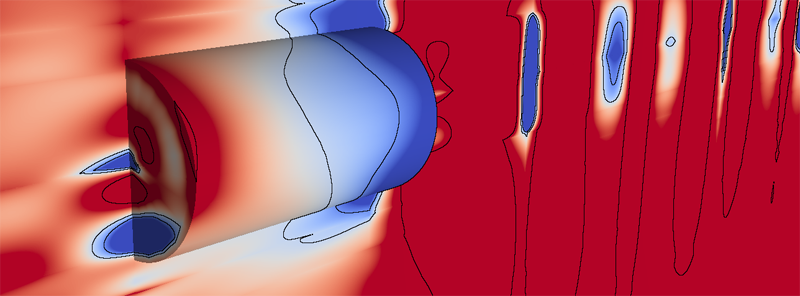
B. Nelson, R. Haimes, R.M. Kirby.
“GPU-Based Interactive Cut-Surface Extraction From High-0rder Finite Element Fields,” In IEEE Transactions on Visualization and Computer Graphics (IEEE Visualization Issue), Vol. 17, No. 12, pp. 1803--1811. 2011.
D.J. Swenson, S.E. Geneser, J.G. Stinstra, R.M. Kirby, R.S. MacLeod.
“Cardiac Position Sensitivity Study in the Electrocardiographic Forward Problem Using Stochastic Collocation and Boundary Element Methods,” In Annals of Biomedical Engineering, Vol. 39, No. 12, pp. 2900--2910. 2011.
DOI: 10.1007/s10439-011-0391-5
PubMed ID: 21909818
PubMed Central ID: PMC336204
The electrocardiogram (ECG) is ubiquitously employed as a diagnostic and monitoring tool for patients experiencing cardiac distress and/or disease. It is widely known that changes in heart position resulting from, for example, posture of the patient (sitting, standing, lying) and respiration significantly affect the body-surface potentials; however, few studies have quantitatively and systematically evaluated the effects of heart displacement on the ECG. The goal of this study was to evaluate the impact of positional changes of the heart on the ECG in the specific clinical setting of myocardial ischemia. To carry out the necessary comprehensive sensitivity analysis, we applied a relatively novel and highly efficient statistical approach, the generalized polynomial chaos-stochastic collocation method, to a boundary element formulation of the electrocardiographic forward problem, and we drove these simulations with measured epicardial potentials from whole-heart experiments. Results of the analysis identified regions on the body-surface where the potentials were especially sensitive to realistic heart motion. The standard deviation (STD) of ST-segment voltage changes caused by the apex of a normal heart, swinging forward and backward or side-to-side was approximately 0.2 mV. Variations were even larger, 0.3 mV, for a heart exhibiting elevated ischemic potentials. These variations could be large enough to mask or to mimic signs of ischemia in the ECG. Our results suggest possible modifications to ECG protocols that could reduce the diagnostic error related to postural changes in patients possibly suffering from myocardial ischemia.
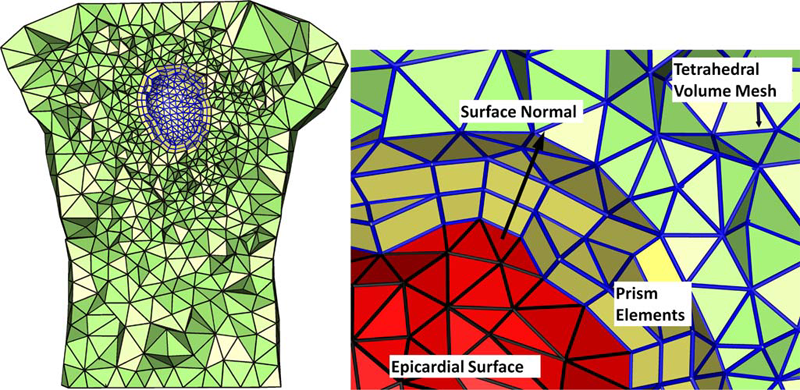
D. Wang, R.M. Kirby, C.R. Johnson.
“Finite Element Based Discretization and Regularization Strategies for 3D Inverse Electrocardiography,” In IEEE Transactions for Biomedical Engineering, Vol. 58, No. 6, pp. 1827--1838. 2011.
PubMed ID: 21382763
PubMed Central ID: PMC3109267
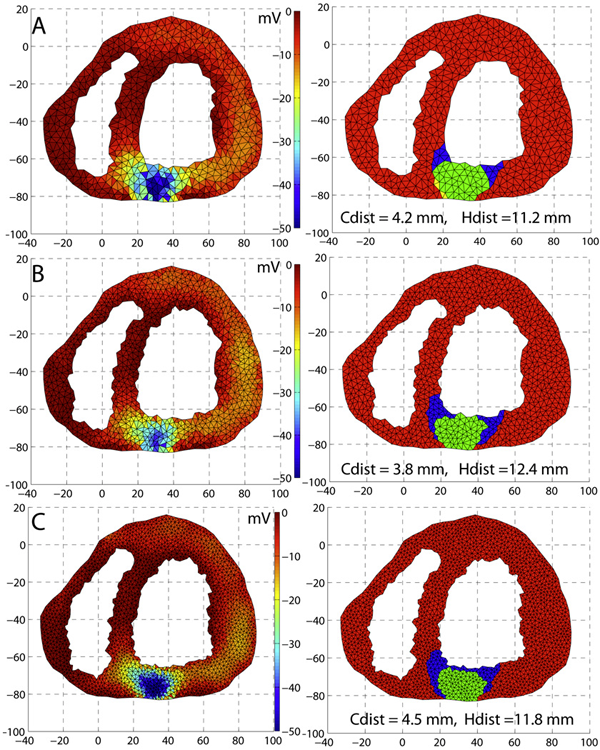
D. Wang, R.M. Kirby, R.S. Macleod, C.R. Johnson.
“An optimization framework for inversely estimating myocardial transmembrane potentials and localizing ischemia,” In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS), pp. 1680--1683. 2011.
DOI: 10.1109/IEMBS.2011.6090483
PubMed ID: 22254648
PubMed Central ID: PMC3336368
C. Yang, D. Xiu, R.M. Kirby.
“Visualization of Covariance and Cross-covariance Field,” In International Journal for Uncertainty Quantification, Vol. 3, No. 1, pp. 25--38. 2011.
DOI: 10.1615/Int.J.UncertaintyQuantification.2011003369
Keywords: netl
2010
T. Etiene, L.G. Nonato, C.E. Scheidegger, J. Tierny, T.J. Peters, V. Pascucci, R.M. Kirby, C.T. Silva.
“Topology Verification for Isosurface Extraction,” SCI Technical Report, No. UUSCI-2010-003, SCI Institute, University of Utah, 2010.
S.E. Geneser, J.D. Hinkle, R.M. Kirby, Brian Wang, B. Salter, S. Joshi.
“Quantifying Variability in Radiation Dose Due to Respiratory-Induced Tumor Motion,” In Medical Image Analysis, Vol. 15, No. 4, pp. 640--649. 2010.
DOI: 10.1016/j.media.2010.07.003
P.K. Jimack, R.M. Kirby.
“Towards the Development on an h-p-Refinement Strategy Based Upon Error Estimate Sensitivity,” In Computers and Fluids, Vol. 46, No. 1, pp. 277--281. 2010.
DOI: 10.1016/j.compfluid.2010.08.003
The use of (a posteriori) error estimates is a fundamental tool in the application of adaptive numerical methods across a range of fluid flow problems. Such estimates are incomplete however, in that they do not necessarily indicate where to refine in order to achieve the most impact on the error, nor what type of refinement (for example h-refinement or p-refinement) will be best. This paper extends preliminary work of the authors (Comm Comp Phys, 2010;7:631–8), which uses adjoint-based sensitivity estimates in order to address these questions, to include application with p-refinement to arbitrary order and the use of practical a posteriori estimates. Results are presented which demonstrate that the proposed approach can guide both the h-refinement and the p-refinement processes, to yield improvements in the adaptive strategy compared to the use of more orthodox criteria.
Page 5 of 10
