SCIENTIFIC COMPUTING AND IMAGING INSTITUTE
at the University of Utah

Seamless image cloning has become one of the most important editing operation for photomontage. Recent coordinate-based methods have lessened considerably the computational cost of image cloning, thus enabling interactive applications. However, those techniques still bear severe limitations as to concavities and dynamic shape deformation. In this paper we present novel methodology for image cloning that turns out to be highly efficient in terms of computational times while still being more flexible than existing techniques. Our approach builds on combinatorial Laplacian and fast Cholesky factorization to ensure interactive image manipulation, handling holes, concavities, and dynamic deformations during the cloning process. The provided experimental results show that the proposed technique outperforms existing methods in requisites such as accuracy and flexibility.

The broad goals of verifiable visualization rely on correct algorithmic implementations. We extend a framework for verification of isosurfacing implementations to check topological properties. Specifically, we use stratified Morse theory and digital topology to design algorithms which verify topological invariants. Our extended framework reveals unexpected behavior and coding mistakes in popular publicly-available isosurface codes.

This video presents a visualization of a recent algorithm to compute discrete gradient fields on regular cell complexes [3]. Discrete gradient fields are used in practical methods that robustly translate smooth Morse theory to combinatorial domains. We describe the stages of the algorithm, highlighting both its simplicity and generality.

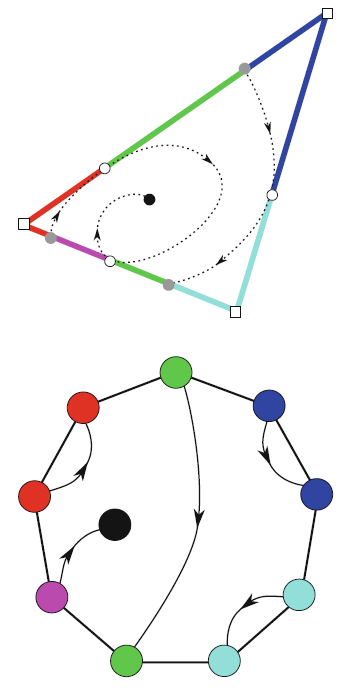
Typically, vector fields are stored as a set of sample vectors at discrete locations. Vector values at unsampled points are defined by interpolating some subset of the known sample values. In this work, we consider two-dimensional domains represented as triangular meshes with samples at all vertices, and vector values on the interior of each triangle are computed by piecewise linear interpolation.

Many of the commonly used techniques for studying properties of the vector field require integration techniques that are prone to inconsistent results. Analysis based on such inconsistent results may lead to incorrect conclusions about the data. For example, vector field visualization techniques integrate the paths of massless particles (streamlines) in the flow or advect a texture using line integral convolution (LIC). Techniques like computation of the topological skeleton of a vector field, require integrating separatrices, which are streamlines that asymptotically bound regions where the flow behaves differently. Since these integrations may lead to compound numerical errors, the computed streamlines may intersect, violating some of their fundamental properties such as being pairwise disjoint. Detecting these computational artifacts to allow further analysis to proceed normally remains a significant challenge.

We present a set of building blocks that provide scalable data movement capability to computational scientists and visualization researchers for writing their own parallel analysis. The set includes scalable tools for domain decomposition, process assignment, parallel I/O, global reduction, and local neighborhood communicationtasks that are common across many analysis applications. The global reduction is performed with a new algorithm, described in this paper, that efficiently merges blocks of analysis results into a smaller number of larger blocks. The merging is configurable in the number of blocks that are reduced in each round, the number of rounds, and the total number of resulting blocks. We highlight the use of our library in two analysis applications: parallel streamline generation and parallel Morse-Smale topological analysis. The first case uses an existing local neighborhood communication algorithm, whereas the latter uses the new merge algorithm.

Gradient domain processing remains a particularly computationally expensive technique even for relatively small images. When images become massive in size, giga or terapixel, these problems become particularly troublesome and the best serial techniques take on the order of hours or days to compute a solution. In this paper, we provide a simple framework for the parallel gradient domain processing. Specifically, we provide a parallel out-of-core method for the seamless stitching of gigapixel panoramas in a parallel MPI environment. Unlike existing techniques, the framework provides both a straightforward implementation, maintains strict control over the required/allocated resources, and makes no assumptions on the speed of convergence to an acceptable image. Furthermore, the approach shows good weak/strong scaling from several to hundreds of cores and runs on a variety of hardware.

Gradient domain processing is a computationally expensive image processing technique. Its use for processing massive images, giga or terapixels in size, can take several hours with serial techniques. To address this challenge, parallel algorithms are being developed to make this class of techniques applicable to the largest images available with running times that are more acceptable to the users. To this end we target the most ubiquitous form of computing power available today, which is small or medium scale clusters of commodity hardware. Such clusters are continuously increasing in scale, not only in the number of nodes, but also in the amount of parallelism available within each node in the form of multicore CPUs and GPUs. In this paper we present a hybrid parallel implementation of gradient domain processing for seamless stitching of gigapixel panoramas that utilizes MPI, threading and a CUDA based GPU component. We demonstrate the performance and scalability of our implementation by presenting results from two GPU clusters processing two large data sets.

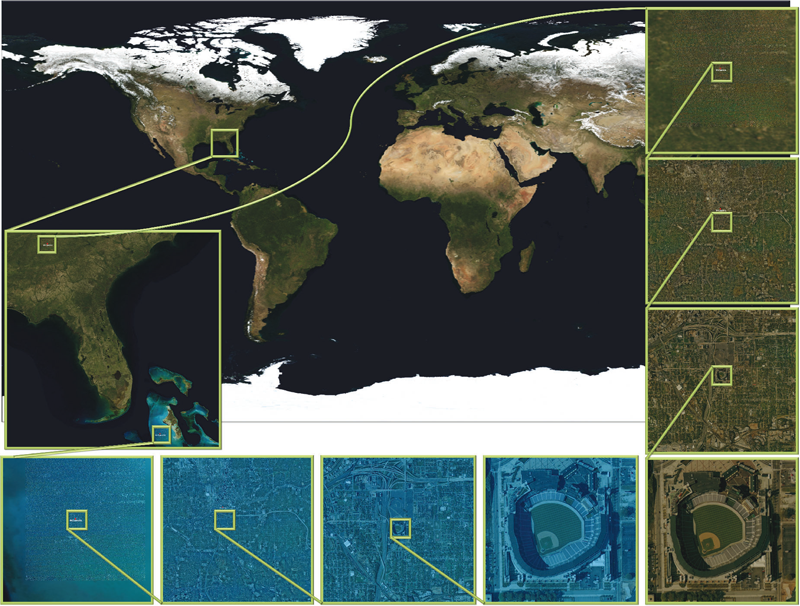
This article presents a simple framework for progressive processing of high-resolution images with minimal resources. We demonstrate this framework's effectiveness by implementing an adaptive, multi-resolution solver for gradient-based image processing that, for the first time, is capable of handling gigapixel imagery in real time. With our system, artists can use commodity hardware to interactively edit massive imagery and apply complex operators, such as seamless cloning, panorama stitching, and tone mapping.

We introduce a progressive Poisson solver that processes images in a purely coarse-to-fine manner, providing near instantaneous global approximations for interactive display (see Figure 1). We also allow for data-driven adaptive refinements to locally emulate the effects of a global solution. These techniques, combined with a fast, cache-friendly data access mechanism, allow the user to interactively explore and edit massive imagery, with the illusion of having a full solution at hand. In particular, we demonstrate the interactive modification of gigapixel panoramas that previously required extensive offline processing. Even with massive satellite images surpassing a hundred gigapixels in size, we enable repeated interactive editing in a dynamically changing environment. Images at these scales are significantly beyond the purview of previous methods yet are processed interactively using our techniques. Finally our system provides a robust and scalable out-of-core solver that consistently offers high-quality solutions while maintaining strict control over system resources.

Large-scale visualization systems are typically designed to efficiently \"push\" datasets through the graphics hardware. However, exploratory visualization systems are increasingly expected to support scalable data manipulation, restructuring, and querying capabilities in addition to core visualization algorithms. We posit that new emerging abstractions for parallel data processing, in particular computing clouds, can be leveraged to support large-scale data exploration through visualization. In this paper, we take a first step in evaluating the suitability of the MapReduce framework to implement large-scale visualization techniques. MapReduce is a lightweight, scalable, general-purpose parallel data processing framework increasingly popular in the context of cloud computing. Specifically, we implement and evaluate a representative suite of visualization tasks (mesh rendering, isosurface extraction, and mesh simplification) as MapReduce programs, and report quantitative performance results applying these algorithms to realistic datasets. For example, we perform isosurface extraction of up to l6 isovalues for volumes composed of 27 billion voxels, simplification of meshes with 30GBs of data and subsequent rendering with image resolutions up to 80000² pixels. Our results indicate that the parallel scalability, ease of use, ease of access to computing resources, and fault-tolerance of MapReduce offer a promising foundation for a combined data manipulation and data visualization system deployed in a public cloud or a local commodity cluster.

Keywords: MapReduce, Hadoop, cloud computing, large meshes, volume rendering, gigapixels

Large observations and simulations in scientific research give rise to high-dimensional data sets that present many challenges and opportunities in data analysis and visualization. Researchers in application domains such as engineering, computational biology, climate study, imaging and motion capture are faced with the problem of how to discover compact representations of high dimensional data while preserving their intrinsic structure. In many applications, the original data is projected onto low-dimensional space via dimensionality reduction techniques prior to modeling. One problem with this approach is that the projection step in the process can fail to preserve structure in the data that is only apparent in high dimensions. Conversely, such techniques may create structural illusions in the projection, implying structure not present in the original high-dimensional data. Our solution is to utilize topological techniques to recover important structures in high-dimensional data that contains non-trivial topology. Specifically, we are interested in high-dimensional branching structures. We construct local circle-valued coordinate functions to represent such features. Subsequently, we perform dimensionality reduction on the data while ensuring such structures are visually preserved. Additionally, we study the effects of global circular structures on visualizations. Our results reveal never-before-seen structures on real-world data sets from a variety of applications.

Keywords: Dimensionality reduction, circular coordinates, visualization, topological analysis

In this work we introduce a new hierarchical surface decomposition method for multiscale analysis of surface meshes. In contrast to other multiresolution methods, our approach relies on spectral properties of the surface to build a binary hierarchical decomposition. Namely, we utilize the first nontrivial eigenfunction of the Laplace–Beltrami operator to recursively decompose the surface. For this reason we coin our surface decomposition the Fiedler tree. Using the Fiedler tree ensures a number of attractive properties, including: mesh-independent decomposition, well-formed and nearly equi-areal surface patches, and noise robustness. We show how the evenly distributed patches can be exploited for generating multiresolution high quality uniform meshes. Additionally, our decomposition permits a natural means for carrying out wavelet methods, resulting in an intuitive method for producing feature-sensitive meshes at multiple scales.