Femoroacetabular impingement (FAI) is caused by reduced clearance between the femoral head and acetabulum due to anatomic abnormalities of the femur (cam FAI), acetabulum (pincer FAI), or both (mixed FAI). Cam FAI is characterized by an aspherical femoral head or reduced femoral head-neck offset. During hip flexion, the abnormally shaped femur may cause shearing at the chondrolabral junction, thereby damaging articular cartilage and the acetabular labrum. Currently, diagnosis of cam FAI is largely accomplished using two-dimensional (2D) measurements of femur morphology acquired from radiographic projections or a series of radial planes from computed tomography (CT) or magnetic resonance (MR) images. Two- dimensional measures provide initial diagnosis of cam FAI, but their reliability has been debated. Also, there is no agreement on the range of measurements that should be considered normal. Furthermore, radiographic measures give only a limited description of femur anatomy or shape variation among cam FAI deformities. Together, these limitations of 2D measurements translate into a high misdiagnosis rate. In a series of FAI patients treated with surgery in our clinic, 40% had seen multiple previous musculoskeletal providers and 15% had undergone surgical procedures unrelated to the hip joint (hernia, etc.).

Mean control (left) and cam (right) shapes. Middle images show the mean control shape with color plots depicting how the mean cam shape differed across the femoral head, neck, and proximal shaft. Top and bottom rows show different rotations of the femoral head.	Volumetric CT images from a cam FAI patient. Validated threshold settings were applied to CT images to segment and reconstruct the bony morphology of each femur.

Three-dimensional (3D) femur reconstructions from CT images can visualize the entire femoral head. However, evaluations of cam FAI using 3D femur reconstructions have relied on the questionable assumption that a sphere is the ideal femoral head shape. In contrast, statistical shape modeling (SSM) can be applied to 3D reconstructions to objectively compare complex morphology without idealizing underlying geometry. Prior orthopaedic applications of SSM have included analyses of tibiofemoral and patellofemoral joints and methods to reconstruct femur or pelvis shape from sparse image data. Most SSM strategies distribute a labeled set of points across representative shapes for a given population. Methods of point placement may involve manual placement at anatomic landmarks, derivation from finite element meshes, or automatic placement based on point-to-point minimization of distance and entropy. Regardless of the method, by optimizing and comparing the positional configurations of the labeled points, SSM can quantify and visualize geometric variation existing within the population.

Application of SSM to a study of cam FAI may facilitate improved diagnosis and preoperative planning. Specifically, SSM can be applied to reconstructions of cam FAI and healthy femurs to generate 3D representatives of the average cam FAI femur compared to the average control. SSM also facilitates quantitative and qualitative analysis of shape variations among femurs, which may have clinical use in describing the spectrum of cam FAI deformities and classifying the severity of deformities on a patient-specific basis.

Statistical Shape Modeling

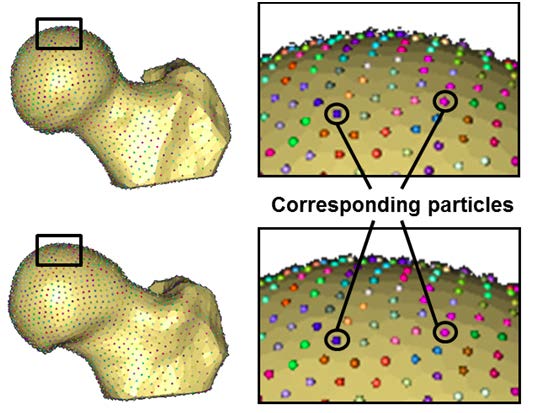
The objective of this project was to generate accurate 3D reconstructions of femoral heads from volumetric CT images and apply SSM to quantify 3D variation and morphologic differences between femurs with and without cam FAI. A basic principle of most SSMs is to place particles at corresponding locations on every shape in the population of interest. The SSM method used has been described in detail by Cates (1).

After a 3D reconstruction and SSP preprocessing, the method iteratively moves a system of dynamic particles across the surfaces to find positions that optimize the information content of the system. Binary segmentations of the femur were preprocessed to remove aliasing artifacts, and 2048 particles (aka correspondences) were initialized and optimized on each femur (Figure~\ref{fig:Corresp}), using a splitting strategy. This strategy proceeded by randomly choosing a surface location and there placing a single particle that was then split to produce a second, nearby particle. Initial locations of the two particles were determined using a system of repulsive forces until a steady state between the particles was achieved. The splitting process and steady state initialization were repeated until 2048 particles were placed on each surface.

Until recently, most SSM correspondences for shape statistics were established manually by choosing small sets of anatomically significant landmarks on regions of interest, which would then serve as the basis for shape analysis. The demand for more detailed analyses on ever larger populations of subjects has rendered this approach increasingly difficult. The current study used a method presented by Cates (2) for extracting dense sets of correspondences that describe large ensembles of similar shapes. Thus instead of a reliance on relatively few correspondences or the necessity for training shapes, correspondence positions in this study resulted in a geometrically accurate sampling of individual shapes, while computing a statistically simple model of the ensemble. Because of this advantage over previous SSM techniques, we are easily able to increase the number of correspondences used and the number of femurs included in the analysis, both of which are part of our future work.

Quantification of Anatomical Variations

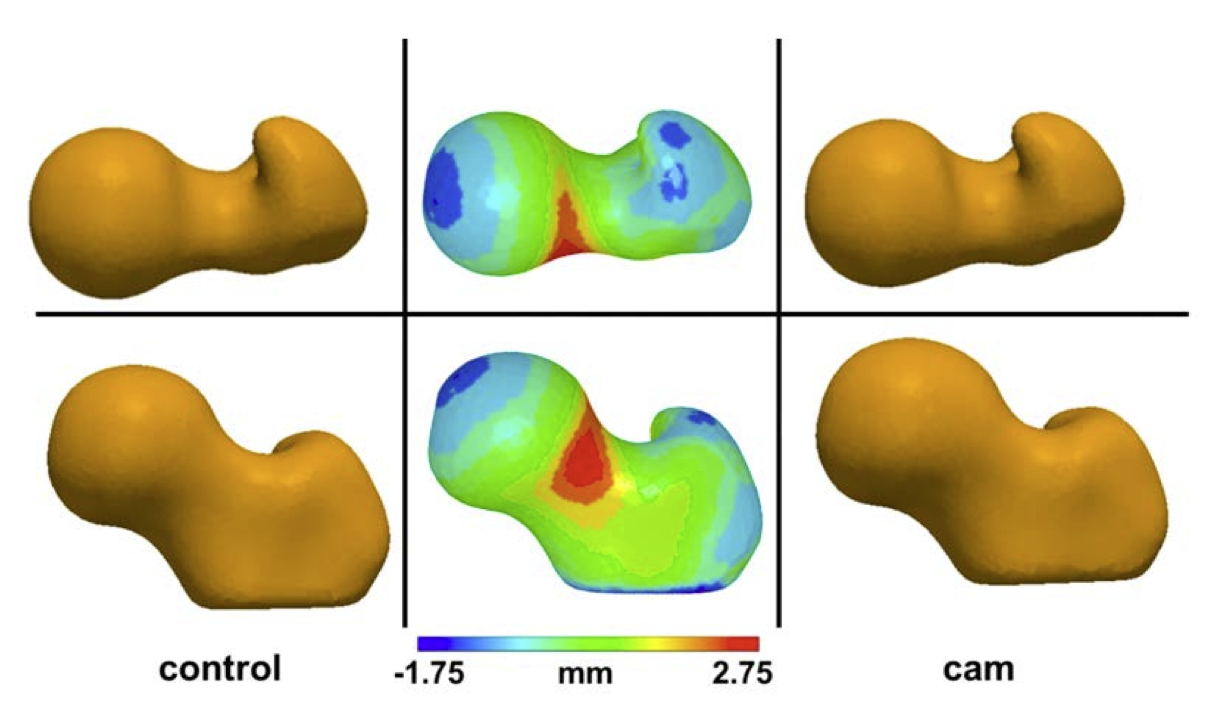
This study used SSM to quantify and compare femoral head morphology between control and cam FAI femurs.

Correspondence particle distribution on a control and a cam FAI femur. 2048 particles were placed on each femur and optimally positioned to balance model compactness and accurate shape representation.

The primary result of this study was the computation of mean femoral shapes for controls and cam FAI patients. The greatest differences between the mean shapes were located along the anterolateral head-neck junction (figure at the top), which corresponds very well with clinical findings of cam lesions locations and intraoperative findings of damage to the articular cartilage and labrum. The mean shapes, as well as color plotted differences of individual cam femurs compared to the mean shapes, can serve as a quantitative road map for the location and amount of debridement required to restore a cam femur to a normal shape.

Considerable variation was found in the shape and height of the greater trochanter, among all femurs and between groups. There were also large variations among femurs in the distance between the greater trochanter and the center of the femoral head (i.e., femoral offset) as well as the diameter of the femoral neck. This finding alone demonstrates the potential utility of SSM for objectively describing variations in femoral shape and the spectrum of possible deformities, which would otherwise be difficult to identify using traditional radiographs.

Cam FAI can be painful and has the potential to shorten the lifetime of a native hip through degeneration of articular cartilage and separation of the cartilage from the acetabular labrum. Current hip preservation surgeries seek to mitigate damage by removing cam lesions and increasing head-neck concavity. Under correction of a cam lesion may cause lingering pain and could require revision surgery, while over correction could endanger the mechanical integrity or blood supply of the femur.

The use of statistical shape modeling with control and cam FAI femurs, as done in our current research, allows physicians to visualize individual cam lesions in context with average normal and pathologic shapes. Our control and cam femur databases are continually growing, thus improving the strength of the statistically determined shapes. SSM of cam FAI avoids the assumption that healthy femurs are spherical and allows objective determination of true femoral shape among normal and pathologic populations. Use of SSM of cam FAI in the clinical setting not only could improve our understanding of femoral morphology but also may provide more exact diagnoses and improved preoperative planning.

References:

(1) J. Cates, P.T. Fletcher, M. Styner, M. Shenton, and R.T. Whitaker. Shape modeling and analy- sis with entropy-based particle systems. In Proceedings of Information Processing in Medical Imaging (IPMI) 2007, LNCS 4584, pages 333–345, 2007.

(2) J. Cates, M.D. Meyer, P.T. Fletcher, and R.T. Witaker. Entropy-based particle systems for shape correspondence. In Workshop on Mathematical Foundations of Computational Anatomy, MIC- CAI 2006, pages 90–99, October 2006.