University of Utah

Courses

List of All Courses by Topics:

	Machine Learning:	Machine Learning
	Statistics:	Nonparametric Methods, Statistics for Biomedical Informatics
	Computer Vision:	3D Computer Vision, Image Processing, Advanced Image Processing
	Scientific Computing:	Advanced Scientific Computation I, Advanced Scientific Computation II
	Math:	Introduction to Partial Differential Equations, Introduction to Riemannian Manifolds
	Imaging:	Mathematics of Imaging, Principles of Magnetic Resonance Imaging
	Graphics:	Interactive Computer Graphics, Scientific Visualization
	Algorithm:	Advanced Algorithm
	English:	Advanced Pronunciation and Oral Skills, Scientific Writing, Writing for Publication
	Others:	Introduction to Human/Computer Interaction

Selected Course Projects

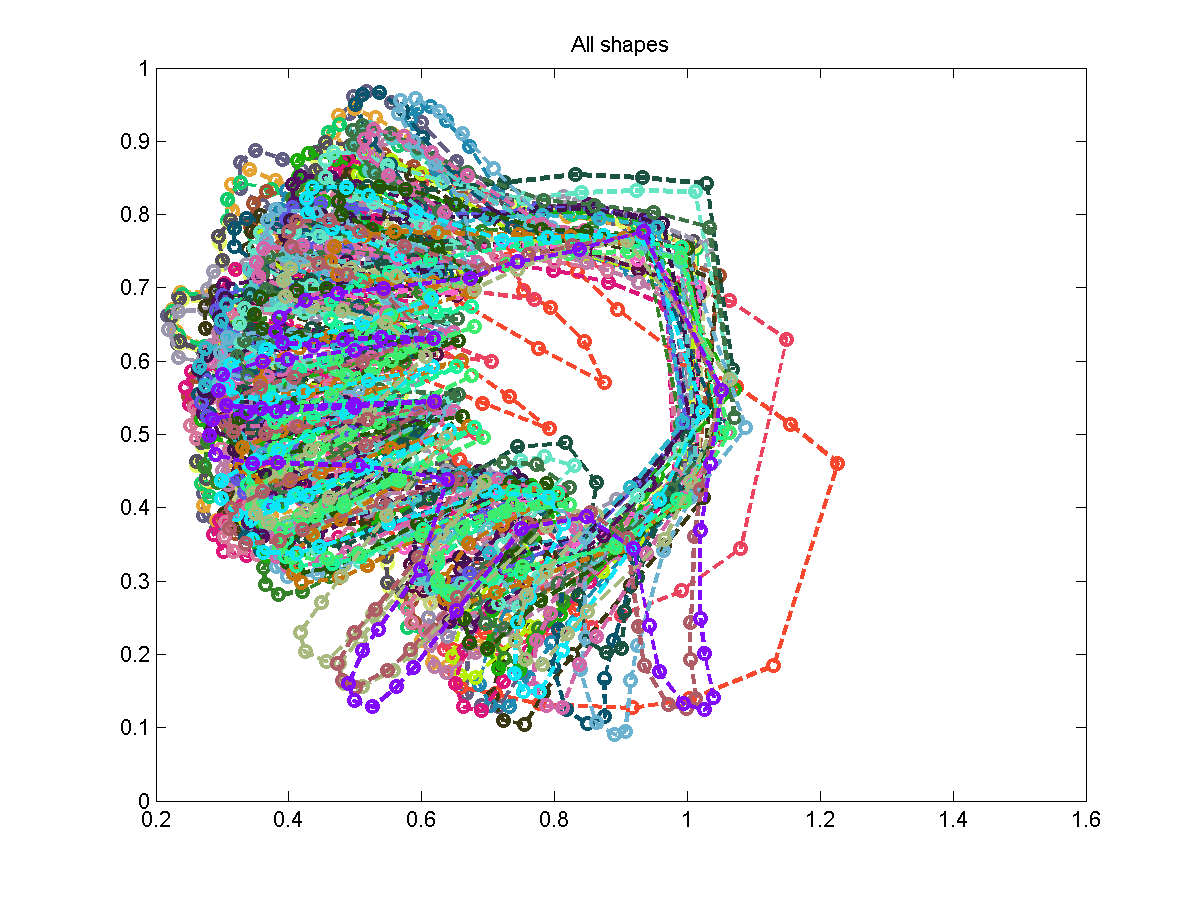
All Shapes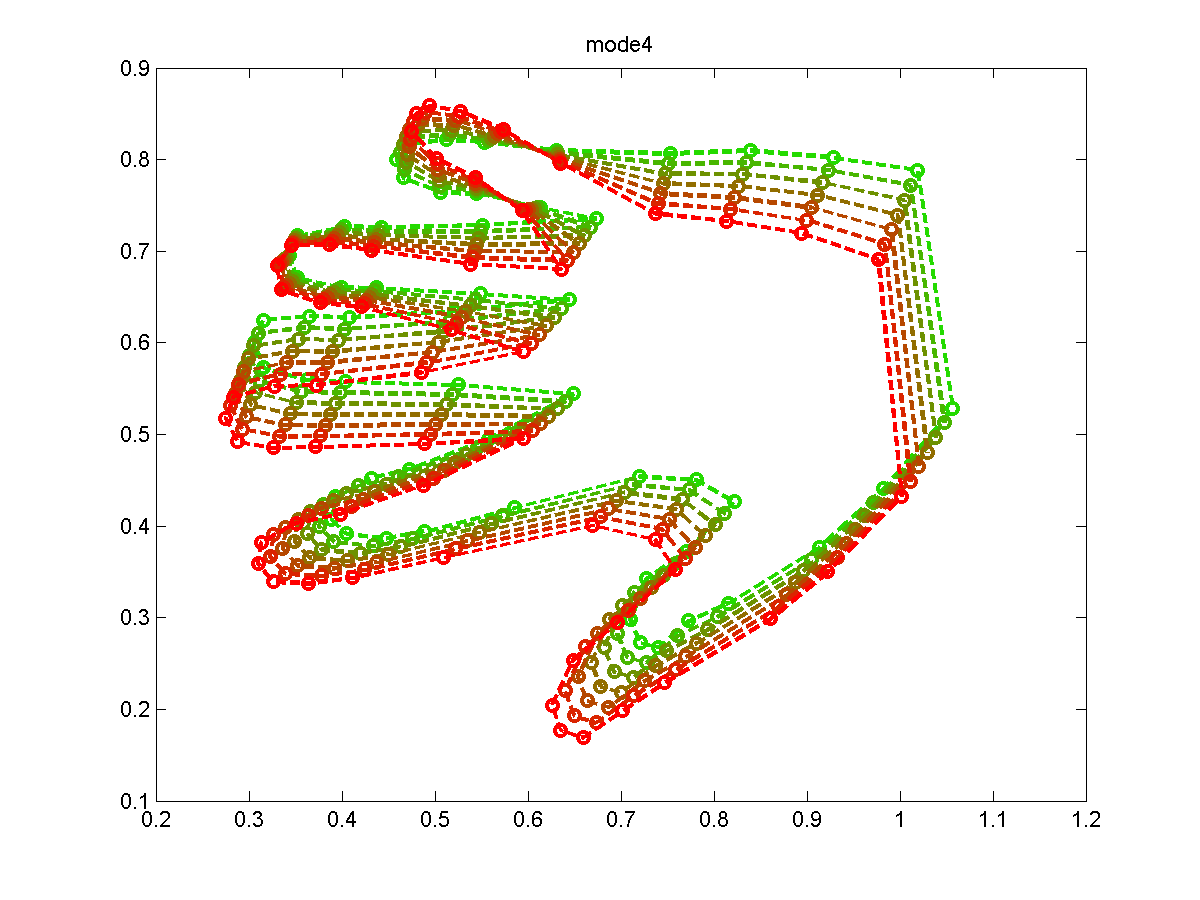 One Mode

Active Shape Model Given a set of shapes represented by Point Distribution Model (PDM), we use a principal component analysis (PCA) to determine the principal shape variations in the population of shapes. Each eigenvector describes a mode of variation whereas the corresponding eigenvalue determines the magnitude of the variation. By truncating the major set of eigenvalues with corresponding eigenvectors, shapes can be represented by a small set of coefficients.

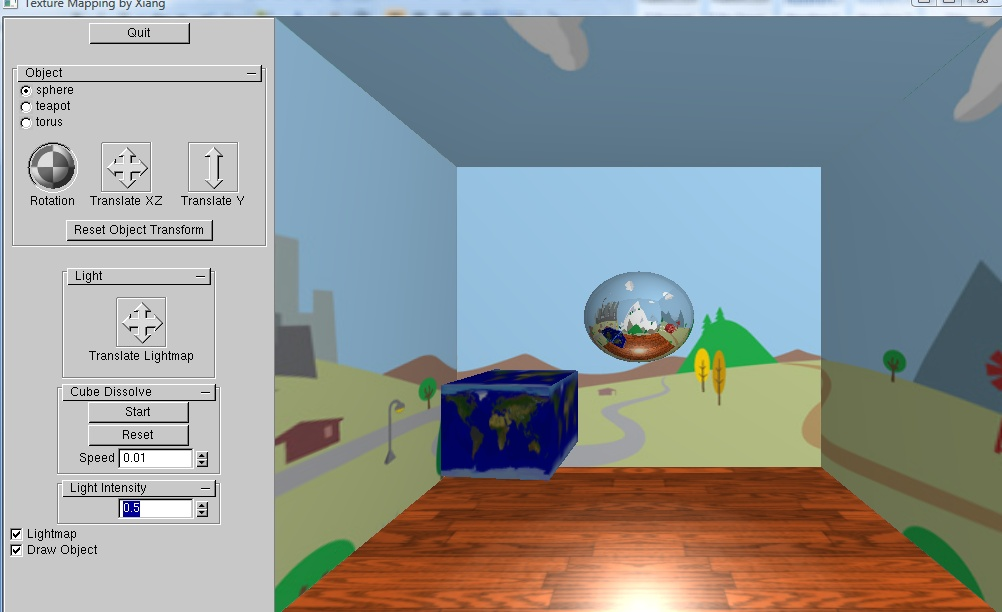
Software Interface Texture Mapping

Texture Mapping Implement a white point light source (positional) using the OpenGL lighting model. Include a 4-sided room such that one wall does not appear. Place a cube in the center of the room, and this cube is appropriate scaled and texture-mapped with the image of the environment. Include GLUI functions that control the speed of a dissolve, and a lightmap with multi-texturing for the floor.

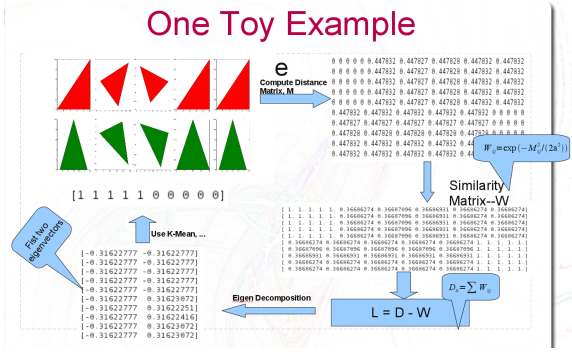
Analysis pipeline

2D Shape Analysis with Spectral Clustering The goal of this project is to compute the distance between similar shapes, and to separate the shapes using spectral clustering. To compute the distance of shapes, we first transform the shape vectors into Kendall Shape Space, and then the distance between shapes, invariant with rotation, translation, scaling, is computed. Next, we incorporate the computed distance into spectral clustering to cluster all the shapes into different groups.

Hypothesis Testing (The image is from here )

Hypothesis Testing Study the permutation test. Simulate the Type I and Type II error rate for the parametric t-test and a permutation test of the t statistics. Use Fisher's Transformation to test a hypothesis about correlation.

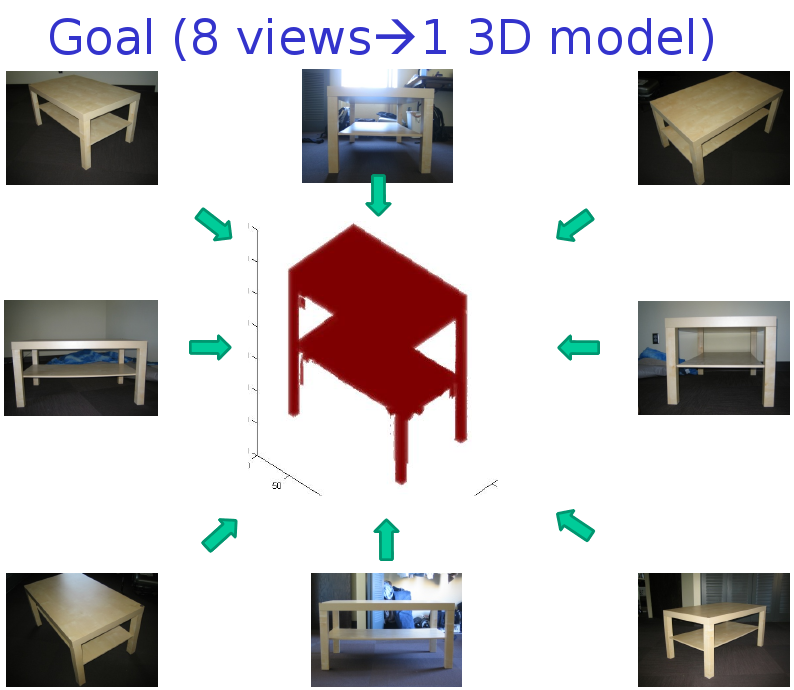
3D Shape from Silhouettes

3D Shape from Silhouettes In this project, we want to compute 3D shapes from several silhouette images. First of all, we compute the projection transformations from the world coordinates to each image space(several different views) by finding correspondent points in image space and world space. Next, each 3D voxel in the world coordinates is transformed to image spaces, where the information is pulled back to the world coordinates. After having visited all voxels, we finally visualize the 3D volume.

Courses Details:

CS 6150 - Advanced Algorithm, Fall 2011

Prof. Suresh Venkatasubramanian

Assignment 1: Divide and Conquer
Assignment 2: Dynamic Programming
Assignment 3: Network Flows
Assignment 4: Randomized Algorithms
Assignment 5: Complexity Theory and Approximation Algorithm Design

WRTG 7060 - Scientific Writing, Fall 2011

Prof. James K Koford

CS 6220 - Advanced Scientific Computation II, Spring 2011

Prof. Christopher (Krzysztof) Sikorski

Homework 1: Linear Least Squares Problem
Homework 2: Eigenvalue Problems
Homework 3: Data Compression via SVD Decomposition
Homework 4: Interpolation and Integration Methods
Homework 5: Differential Equations

Bioen 6500 - Mathematics of Imaging, Spring 2011

Prof. Sarang Joshi

Project 1: Image Denoising
Project 2: Image Deconvolution
Project 3: Diffusion Tensor Imaging Denoising

CS 7931 - Introduction to Riemannian Manifolds(Seminar), Spring 2011

Prof. Tom Fletcher

Course content: Riemannian Metrics, Affine Connections, Riemannian Connections, Geodesics.

WRTG 6000 - Writing for Publication, Spring 2011

Prof. Paul Laurence Ketzle

CS 6210 - Advanced Scientific Computation I, Fall 2010

Prof. Christopher (Krzysztof) Sikorski

Homework 1: Floating point arithmetic & Stable and Well behaved algorithms
Homework 2: Solve Dense Linear System
Homework 3: Solve Sparse Linear System
Homework 4: Solve Nonlinear Equations

Math 6850/5440 - Introduction to Partial Differential Equations, Fall 2010

Prof. Nick Korevaar

Course content: Vector calculus, PDE derivations, Solving linear PDE(BVP, IBVP), Fourier series, Fourier series solutions to PDE, Green's functions solutions to PDE, Hilbert Spaces and the spectral theorem.

CS 7960 - Advanced Image Processing, Spring 2010

Prof. Guido Gerig

Project 1: Blob detection by scale space filtering
Project 2: Anisotropic Diffusion
Project 3: Contour Descriptors from Elliptic Harmonics
Project 4: Active Shape Models ASMs
Project 5: Snakes: Deformable Contour Segmentation
Project 6: Normalized Graph Cuts

CS 7931 - Introduction to Riemannian Manifolds(Seminar), Spring 2010

Prof. Tom Fletcher

Course content: Topoly, Differentiable Manifolds, Riemannian Geometry, Lie Groups.

BIOEN 6330 - Principles of Magnetic Resonance Imaging, Spring 2010

Prof. Edward W. Hsu

Assignment 1
Assignment 2
Assignment 3
Assignment 4
Assignment 5

BMI 6105 - Statistics for Biomedical Informatics, Spring 2010

Prof. Jones J. P.

Course content: Descriptive Summary, Graphical Summary, T-test/Wilcoxon Test, Prop Test/Binomial Test, Chi-square Test/Fisher Test, Correlation(Pearson and Spearman), Linear Regression and Multivariate Linear Regression, ANOVA(Analysis of Variance), General Linear Model and Logistic Regression, Survival Analysis, Cox Test, Resampling Methods and Interaction.

CS 6350 - Machine Learning, Fall 2009

Prof. Hal Daumé III

Project 0: Unix/Python/NumPy tutorial
Project 1: Linear models
Project 2: Features and Kernels
Project 3: Unsupervised learning
Project 4: Text modeling
Final Project: 2D Shape Analysis with Spectral Clustering

CS 6968 3D Computer Vision, Fall 2009

Prof. Guido Gerig

Assignment 1: Geometric Camera Calibration
Assignment 2: Photometric Stereo / Multiple View Stereo
Assignment 3: Structured Light/ Motion and Optic Flow
Final Project: 3D Shape from Silhouettes

CS 6960 - Nonparametric Methods, Spring 2009

Prof. Tom Fletcher

Homework 1: Expectation and Simulation
Homework 2: Generating Random Variables
Homework 3: Estimates for the Gaussian CDF
Homework 4: Monte Carlo and Variance Reduction
Homework 5: The Bootstrap and Jackknife
Homework 6: Hypothesis Testing
Final Project: Simulation of the Activation Detection in fMRI

CS/BIONENG 6640 - Image Processing, Spring 2009

Prof. Ross T. Whitaker

Project 1: Histogram and Connected Components Analysis with Topological Denoising
Project 2: Histogram Equalization, Adaptive Histogram Equalization, and Clipped Local Adaptive Histogram Equalization
Project 3: Image Mosaic Building with Correspondent points
Project 4: Automatically Image Mosaic Building with Phase Correlation and Peak finding
Project 5: Feature and Object Detection

ESL 6300 - Advanced Pronunciation and Oral Skills, Spring 2009

Prof. Hiller, K. E.

CS 6540 - Introduction to Human/Computer Interaction, Fall 2008

Prof. Richard F. Riesenfeld

Assignment 1: Good and bad Interfaces/Functionality
Assignment 2: PBS Nova Video Clip: Face to Face
Assignment 3: Affordance vs. Mapping
Assignment 4: Forcing function
Assignment 5: University of Utah Website Analysis
Assignment 6: Interfaces Analysis
Final Projects: Medical Prescription Manager

CS 6630 - Scientific Visualization, Fall 2008

Prof. Claudio T. Silva

Assignment 0: Basic concepts of the Vistrials System, VTK, and matploitlib
Assignment 1: Basic plotting concepts and produce plots using matplotlib/python/Vistrails
Assignment 2: Visualization of 2D scalar and vector fields
Assignment 3: Visualization of 3D scalar volumes
Assignment 4: Visualization of large graphs
Final Project: Visualization

CS 6610 - Interactive Computer Graphics, Fall 2008

Prof. Charles (Chuck) Hansen

Assignment 1: Texture Mapping
Assignment 2: Projective Shadows, Shadow Maps, and Shadow Volume
Assignment 3: Shaders
Final Project: An Approximate Interactive Refraction